Refine listing
Actions for selected content:
149 results in 30Dxx
Hyperbolic linear invariance and hyperbolic k-convexity
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 1 / February 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 73-93
- Print publication:
- February 1995
-
- Article
-
- You have access
- Export citation
Inequalities and representation formulas for functions of exponential type
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 1 / February 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 15-26
- Print publication:
- February 1995
-
- Article
-
- You have access
- Export citation
Euclidean linear invariance and uniform local convexity
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 52 / Issue 3 / June 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 401-418
- Print publication:
- June 1992
-
- Article
-
- You have access
- Export citation
The spectral theory of multiplication operators and the recurrence properties for nondifferentiable functions in the Zygmund class Λ*a
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 1 / June 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 136-151
- Print publication:
- June 1992
-
- Article
- Export citation
Admissible solutions of the Schwarzian differential equation
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 2 / April 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 258-278
- Print publication:
- April 1991
-
- Article
-
- You have access
- Export citation
On the construction of convergent iterative sequences of polynomials
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 3 / December 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 382-390
- Print publication:
- December 1989
-
- Article
-
- You have access
- Export citation
On Hayman's alternative
- Part of
-
- Journal:
- Mathematika / Volume 32 / Issue 1 / June 1985
- Published online by Cambridge University Press:
- 26 February 2010, pp. 139-146
- Print publication:
- June 1985
-
- Article
- Export citation
Simultaneous Iteration by Entire or Rational Functions and Their Inverses
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 34 / Issue 3 / June 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 364-367
- Print publication:
- June 1983
-
- Article
-
- You have access
- Export citation
The iteration of polynomials and transcendental entire functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 4 / April 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 483-495
- Print publication:
- April 1981
-
- Article
-
- You have access
- Export citation
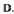 The concept of linear invariance has proved fruitful in geometric function theory. One aspect of Pommerenke's work is the extension of certain results from classical univalent function theory to linearly invariant functions. We propose a definition of a related concept that we call hyperbolic linear invariance for locally schlicht holomorphic functions that map the unit disk into itself. We obtain results for hyperbolic linearly invariant functions which generalize parts of the theory of bounded univalent functions. There are many similarities between linearly invariant functions and hyperbolic linearly invariant functions, but some new phenomena also arise in the study of hyperbolic linearly invariant functions.
The concept of linear invariance has proved fruitful in geometric function theory. One aspect of Pommerenke's work is the extension of certain results from classical univalent function theory to linearly invariant functions. We propose a definition of a related concept that we call hyperbolic linear invariance for locally schlicht holomorphic functions that map the unit disk into itself. We obtain results for hyperbolic linearly invariant functions which generalize parts of the theory of bounded univalent functions. There are many similarities between linearly invariant functions and hyperbolic linearly invariant functions, but some new phenomena also arise in the study of hyperbolic linearly invariant functions.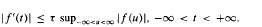 . Moreover we obtain a new representation formula for entire functions of exponential type.
. Moreover we obtain a new representation formula for entire functions of exponential type.
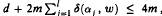 , where α
, where α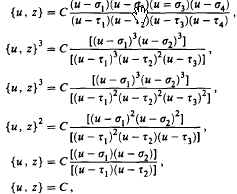
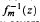 with an arbitrary initial point, where
with an arbitrary initial point, where 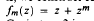 with m ≥ 2. We also show by several counterexamples that Rubinstein's Conjecture 2 is generally false.
with m ≥ 2. We also show by several counterexamples that Rubinstein's Conjecture 2 is generally false.
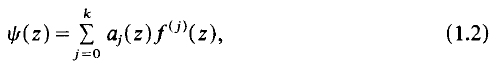
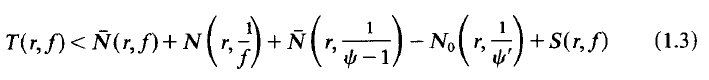
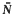
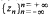 is established which has the properties
is established which has the properties 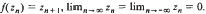 . The result certainly implies
. The result certainly implies 