Refine listing
Actions for selected content:
149 results in 30Dxx
Further results on meromorphic functions that share two values with their derivatives
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 1 / February 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 91-102
- Print publication:
- February 2005
-
- Article
-
- You have access
- Export citation
Normality and exceptional functions of derivatives
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 3 / June 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 403-414
- Print publication:
- June 2004
-
- Article
-
- You have access
- Export citation
A note on normality and shared values
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 1 / February 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 141-150
- Print publication:
- February 2004
-
- Article
-
- You have access
- Export citation
Even and odd entire functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 1 / February 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 19-24
- Print publication:
- February 2003
-
- Article
-
- You have access
- Export citation
About a problem of Hermite and Biehler
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 1 / February 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 87-92
- Print publication:
- February 2002
-
- Article
-
- You have access
- Export citation
On transcendental meromorphic functions which are geometrically finite
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 1 / February 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 93-108
- Print publication:
- February 2002
-
- Article
-
- You have access
- Export citation
Growth of functions in cercles de remplissage
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 1 / February 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 131-136
- Print publication:
- February 2002
-
- Article
-
- You have access
- Export citation
Arakelyan's theorem and relations between two harmonic functions
- Part of
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 February 2010, pp. 301-304
- Print publication:
- December 2001
-
- Article
- Export citation
Weighted composition operators in weighted Banach spaces of analytic functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 1 / August 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 41-60
- Print publication:
- August 2000
-
- Article
-
- You have access
- Export citation
On families of Cauchy transforms and BMOA
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 68 / Issue 3 / June 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 357-364
- Print publication:
- June 2000
-
- Article
-
- You have access
- Export citation
About the zeros of some entire functions and their derivatives
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 68 / Issue 2 / April 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 165-169
- Print publication:
- April 2000
-
- Article
-
- You have access
- Export citation
Functions of bounded expansion: normal and Bloch functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 2 / April 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 168-188
- Print publication:
- April 1999
-
- Article
-
- You have access
- Export citation
On the value distribution of iterated entire functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 1 / February 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 18-31
- Print publication:
- February 1999
-
- Article
-
- You have access
- Export citation
On singular boundary points of complex functions
- Part of
-
- Journal:
- Mathematika / Volume 45 / Issue 1 / June 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 119-133
- Print publication:
- June 1998
-
- Article
- Export citation
Representation formulas for entire functions of exponential type and generalized bernoulli polynomials
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 3 / June 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 307-316
- Print publication:
- June 1998
-
- Article
-
- You have access
- Export citation
Products of spherical derivatives and normal functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 2 / April 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 231-246
- Print publication:
- April 1998
-
- Article
-
- You have access
- Export citation
Value distribution of certain monomials of algebroid functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 62 / Issue 3 / June 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 398-404
- Print publication:
- June 1997
-
- Article
-
- You have access
- Export citation
The locally convex topology on the space of meromorphic functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 3 / December 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 287-303
- Print publication:
- December 1995
-
- Article
-
- You have access
- Export citation
Some local properties of the solutions of second-order differential equations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 2 / October 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 255-265
- Print publication:
- October 1995
-
- Article
-
- You have access
- Export citation
Normal families of holomorphic functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 1 / August 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 112-117
- Print publication:
- August 1995
-
- Article
-
- You have access
- Export citation
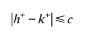
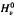 and
and 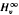 . we estimate the essential norm of a weighted composition operator and compute it for those Banach spaces
. we estimate the essential norm of a weighted composition operator and compute it for those Banach spaces 