Refine listing
Actions for selected content:
149 results in 30Dxx
Ergodic properties of semi-hyperbolic functions with polynomial Schwarzian derivative
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 30 April 2010, pp. 471-502
-
- Article
-
- You have access
- Export citation
THE FILLING DISKS OF AN ALGEBROID FUNCTION IN THE UNIT DISK
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 3 / June 2010
- Published online by Cambridge University Press:
- 25 March 2010, pp. 455-464
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
A NOTE ON VALUE DISTRIBUTION OF DIFFERENCE POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 3 / June 2010
- Published online by Cambridge University Press:
- 05 March 2010, pp. 353-360
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
Rate of growth of frequently hypercyclic functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 12 January 2010, pp. 39-59
-
- Article
-
- You have access
- Export citation
A CLUNIE LEMMA FOR DIFFERENCE AND q-DIFFERENCE POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 02 October 2009, pp. 23-32
- Print publication:
- February 2010
-
- Article
-
- You have access
- Export citation
Integer points of analytic functions in a half-plane
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 3 / October 2009
- Published online by Cambridge University Press:
- 23 September 2009, pp. 619-630
-
- Article
-
- You have access
- Export citation
NORMALITY AND SHARED SETS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 3 / June 2009
- Published online by Cambridge University Press:
- 01 June 2009, pp. 339-354
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
Analytic functions associated with strong Hamburger moment problems
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 02 February 2009, pp. 181-187
-
- Article
-
- You have access
- Export citation
Meromorphic functions with shared limit values of positive linear measure
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 02 February 2009, pp. 235-240
-
- Article
-
- You have access
- Export citation
NEW CHARACTERIZATIONS OF THE MEROMORPHIC BESOV, Qp AND RELATED CLASSES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 09 February 2009, pp. 49-58
- Print publication:
- February 2009
-
- Article
-
- You have access
- Export citation
CONSTRUCTING HERMAN RINGS BY TWISTING ANNULUS HOMEOMORPHISMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 01 February 2009, pp. 139-143
- Print publication:
- February 2009
-
- Article
-
- You have access
- Export citation
ON T DIRECTION OF ALGEBROID FUNCTION DEALING WITH MULTIPLE VALUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 147-156
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
A SECTORIAL THEOREM ON COMPLETELY RAMIFIED RATIONAL FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 131-138
- Print publication:
- February 2008
-
- Article
-
- You have access
- Export citation
Permutable functions concerning differential equations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 3 / December 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 369-384
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
Transcendental meromorphic solutions of some algebraic differential equations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 2 / October 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 157-180
- Print publication:
- October 2007
-
- Article
-
- You have access
- Export citation
Radial distributions of Julia sets of meromorphic functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 3 / December 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 363-368
- Print publication:
- December 2006
-
- Article
-
- You have access
- Export citation
Growth properties and sequences of zeros of analytic functions in spaces of Dirichlet type
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 3 / June 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 397-418
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
Topologies on spaces of vector-valued meromorphic functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 2 / April 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 273-290
- Print publication:
- April 2005
-
- Article
-
- You have access
- Export citation
Multiplicities in Hayman's alternative
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 1 / February 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 37-58
- Print publication:
- February 2005
-
- Article
-
- You have access
- Export citation
On the value distribution of f2f(k)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 1 / February 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 17-26
- Print publication:
- February 2005
-
- Article
-
- You have access
- Export citation
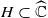 such that (1)
such that (1)