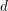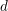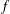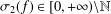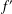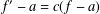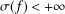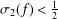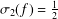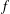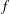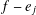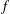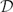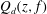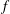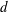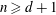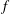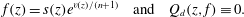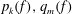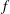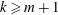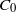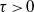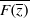Refine listing
Actions for selected content:
149 results in 30Dxx
Hausdorff Dimension of Sets of Escaping Points and Escaping Parameters for Elliptic Functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 30 December 2015, pp. 671-690
-
- Article
- Export citation
Integral points of bounded degree on affine curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 26 November 2015, pp. 754-768
- Print publication:
- April 2016
-
- Article
- Export citation
LOCALISATION OF LINEAR DIFFERENTIAL EQUATIONS IN THE UNIT DISC BY A CONFORMAL MAP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 15 October 2015, pp. 260-271
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
ON THE BRÜCK CONJECTURE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 02 October 2015, pp. 248-259
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
ON UNICITY OF MEROMORPHIC SOLUTIONS TO DIFFERENCE EQUATIONS OF MALMQUIST TYPE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 05 August 2015, pp. 92-98
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
ON THE ESCAPING SET OF MEROMORPHIC FUNCTIONS WITH DIRECT TRACTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 02 April 2015, pp. 68-76
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
The M-set of λ exp(z)/z has infinite area
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 217 / March 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 133-159
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
UNIQUENESS THEOREMS FOR DIRICHLET SERIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 12 February 2015, pp. 389-399
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
GROWTH CONDITIONS FOR OPERATORS WITH SMALLEST SPECTRUM
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 18 December 2014, pp. 665-680
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
ON SOLUTIONS TO NONHOMOGENEOUS ALGEBRAIC DIFFERENTIAL EQUATIONS AND THEIR APPLICATION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 24 September 2014, pp. 391-403
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
REMARKS ON VALUE SHARING OF CERTAIN DIFFERENTIAL POLYNOMIALS OF MEROMORPHIC FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 28 August 2014, pp. 427-443
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
A VARIATION ON SELBERG’S APPROXIMATION PROBLEM
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 14 August 2014, pp. 213-235
- Print publication:
- January 2015
-
- Article
- Export citation
UNIQUENESS OF MEROMORPHIC FUNCTIONS WITH WEAKLY WEIGHTED SHARING
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 28 June 2013, pp. 26-43
- Print publication:
- August 2013
-
- Article
-
- You have access
- Export citation
De Branges’ theorem on approximation problems of Bernstein type
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 12 / Issue 4 / October 2013
- Published online by Cambridge University Press:
- 27 February 2013, pp. 879-899
- Print publication:
- October 2013
-
- Article
- Export citation
A non-Archimedean Montel’s theorem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 21 February 2012, pp. 966-990
- Print publication:
- May 2012
-
- Article
-
- You have access
- Export citation
UNIQUENESS OF MEROMORPHIC FUNCTIONS SHARING ONE VALUE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 04 January 2012, pp. 280-294
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
ON PROPERTIES OF FINITE-ORDER MEROMORPHIC SOLUTIONS OF A CERTAIN DIFFERENCE PAINLEVÉ I EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 08 December 2011, pp. 463-475
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
UNIQUENESS OF ENTIRE FUNCTIONS SHARING A VALUE WITH LINEAR DIFFERENTIAL POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 30 November 2011, pp. 295-306
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
NORMAL FAMILIES OF ZERO-FREE MEROMORPHIC FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 91 / Issue 3 / December 2011
- Published online by Cambridge University Press:
- 16 November 2011, pp. 313-322
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
NONDECREASING FUNCTIONS, EXCEPTIONAL SETS AND GENERALIZED BOREL LEMMAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 3 / June 2010
- Published online by Cambridge University Press:
- 11 June 2010, pp. 353-361
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
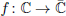 be a non-constant elliptic function. We prove that the Hausdorff dimension of the escaping set of
be a non-constant elliptic function. We prove that the Hausdorff dimension of the escaping set of