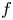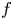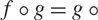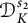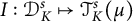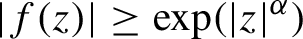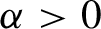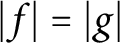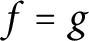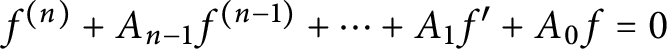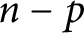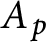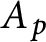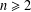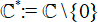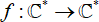Refine listing
Actions for selected content:
149 results in 30Dxx
Non-normality, topological transitivity and expanding families
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 3 / November 2022
- Published online by Cambridge University Press:
- 14 December 2021, pp. 511-523
- Print publication:
- November 2022
-
- Article
- Export citation
A criterion for normality of analytic mappings
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 19 November 2021, pp. 80-88
-
- Article
- Export citation
On unavoidable families of meromorphic functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 18 November 2021, pp. 114-123
- Print publication:
- March 2023
-
- Article
- Export citation
Julia sets of Zorich maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 15 November 2021, pp. 692-728
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Slices of parameter space for meromorphic maps with two asymptotic values
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 18 October 2021, pp. 99-139
- Print publication:
- January 2023
-
- Article
- Export citation
Dual exponential polynomials and a problem of Ozawa
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 16 June 2021, pp. 701-719
- Print publication:
- June 2022
-
- Article
- Export citation
Permutable quasiregular maps
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 1 / July 2022
- Published online by Cambridge University Press:
- 03 June 2021, pp. 105-121
- Print publication:
- July 2022
-
- Article
-
- You have access
- Open access
- Export citation
Characterizations of Morrey type spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 14 May 2021, pp. 328-344
- Print publication:
- June 2022
-
- Article
- Export citation
On the dimension of points which escape to infinity at given rate under exponential iteration
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 5 / May 2022
- Published online by Cambridge University Press:
- 29 March 2021, pp. 1591-1623
- Print publication:
- May 2022
-
- Article
- Export citation
Orbifold expansion and entire functions with bounded Fatou components
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 5 / May 2022
- Published online by Cambridge University Press:
- 04 March 2021, pp. 1807-1846
- Print publication:
- May 2022
-
- Article
-
- You have access
- Open access
- Export citation
Exponential polynomials with Fatou and non-escaping sets of finite Lebesgue measure
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 20 November 2020, pp. 3821-3840
- Print publication:
- December 2021
-
- Article
-
- You have access
- Open access
- Export citation
A note on the phase retrieval of holomorphic functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 08 October 2020, pp. 779-786
- Print publication:
- December 2021
-
- Article
- Export citation
On the number of linearly independent admissible solutions to linear differential and linear difference equations
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 30 July 2020, pp. 1556-1591
- Print publication:
- December 2021
-
- Article
- Export citation
Entropy in uniformly quasiregular dynamics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 22 June 2020, pp. 2397-2427
- Print publication:
- August 2021
-
- Article
- Export citation
Restrictions on meromorphic solutions of Fermat type equations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 3 / August 2020
- Published online by Cambridge University Press:
- 08 May 2020, pp. 654-665
-
- Article
- Export citation
Entire solutions of a variation of the eikonal equation and related PDEs
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 3 / August 2020
- Published online by Cambridge University Press:
- 07 May 2020, pp. 697-708
-
- Article
- Export citation
ON THE PERIODICITY OF TRANSCENDENTAL ENTIRE FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 13 February 2020, pp. 453-465
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
On slow escaping and non-escaping points of quasimeromorphic mappings
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 22 January 2020, pp. 1190-1216
- Print publication:
- April 2021
-
- Article
- Export citation
A note on the topology of escaping endpoints
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 13 January 2020, pp. 1156-1159
- Print publication:
- April 2021
-
- Article
- Export citation
Escaping Fatou components of transcendental self-maps of the punctured plane
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 28 November 2019, pp. 265-289
- Print publication:
- March 2021
-
- Article
- Export citation