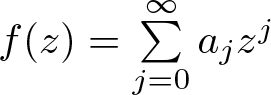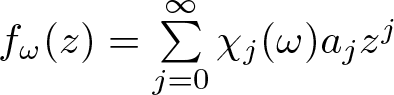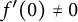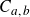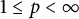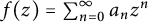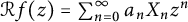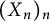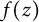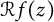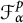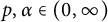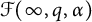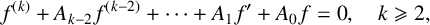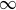Refine listing
Actions for selected content:
149 results in 30Dxx
THE DIFFERENCE ANALOGUE OF THE TUMURA–HAYMAN–CLUNIE THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 145-154
- Print publication:
- August 2024
-
- Article
- Export citation
Normal families and quasiregular mappings
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 23 October 2023, pp. 79-112
-
- Article
- Export citation
Inequalities concerning maximum modulus and zeros of random entire functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 19 October 2023, pp. 57-78
-
- Article
- Export citation
Sparse analytic systems
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 04 July 2023, e58
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Improved Bloch and Landau constants for meromorphic functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 28 April 2023, pp. 1269-1273
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multiply connected wandering domains of meromorphic functions: the pursuit of uniform internal dynamics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 3 / March 2024
- Published online by Cambridge University Press:
- 11 April 2023, pp. 727-748
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BOUNDS FOR FUNCTIONALS DEFINED ON A CERTAIN CLASS OF MEROMORPHIC FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 03 March 2023, pp. 101-109
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multisummability for generalized power series
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 27 February 2023, pp. 458-494
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Iterates of meromorphic functions on escaping Fatou components
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 22 November 2022, pp. 1906-1928
- Print publication:
- December 2023
-
- Article
- Export citation
Topological dynamics of cosine maps
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 23 September 2022, pp. 497-529
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Zero and uniqueness sets for Fock spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 25 July 2022, pp. 532-543
- Print publication:
- June 2023
-
- Article
- Export citation
Two problems on random analytic functions in Fock spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 08 July 2022, pp. 1176-1198
- Print publication:
- August 2023
-
- Article
- Export citation
DESCRIPTION OF GROWTH AND OSCILLATION OF SOLUTIONS OF COMPLEX LDE’S
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 16 June 2022, pp. 145-171
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamics of generalised exponential maps
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 21 April 2022, pp. 123-136
- Print publication:
- January 2023
-
- Article
- Export citation
Generalized Bloch type periodicity and applications to semi-linear differential equations in banach spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 08 March 2022, pp. 326-355
-
- Article
- Export citation
Distinguishing endpoint sets from Erdős space
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 3 / November 2022
- Published online by Cambridge University Press:
- 15 February 2022, pp. 635-646
- Print publication:
- November 2022
-
- Article
- Export citation
CARLSON–GRIFFITHS THEORY FOR COMPLETE KÄHLER MANIFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 14 February 2022, pp. 2337-2365
- Print publication:
- September 2023
-
- Article
- Export citation
On meromorphic solutions of functional-differential equations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 10 February 2022, pp. 263-278
-
- Article
- Export citation
Oscillating simply connected wandering domains
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 4 / April 2023
- Published online by Cambridge University Press:
- 09 February 2022, pp. 1239-1268
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hausdorff dimension of escaping sets of meromorphic functions II
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 03 February 2022, pp. 1471-1491
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation