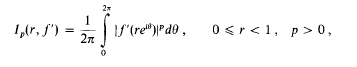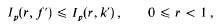Refine listing
Actions for selected content:
543 results in 30xxx
Coefficients of differentially algebraic series
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 48 / Issue 3 / June 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 402-412
- Print publication:
- June 1990
-
- Article
-
- You have access
- Export citation
Complex Clifford analysis and domains of holomorphy
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 48 / Issue 3 / June 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 413-433
- Print publication:
- June 1990
-
- Article
-
- You have access
- Export citation
On the construction of convergent iterative sequences of polynomials
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 3 / December 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 382-390
- Print publication:
- December 1989
-
- Article
-
- You have access
- Export citation
Function classes related to Ruscheweyh derivatives
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 3 / December 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 438-444
- Print publication:
- December 1989
-
- Article
-
- You have access
- Export citation
On discontinuity of l2-angle
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 2 / October 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 269-279
- Print publication:
- October 1989
-
- Article
-
- You have access
- Export citation
Positive Harmonic Functions and Complete Metrics
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 32 / Issue 3 / 01 September 1989
- Published online by Cambridge University Press:
- 20 November 2018, pp. 286-297
- Print publication:
- 01 September 1989
-
- Article
-
- You have access
- Export citation
The last problem of Harald Bohr
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 1 / August 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 133-152
- Print publication:
- August 1989
-
- Article
-
- You have access
- Export citation
Ideals in the Wiener algebra W+
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 46 / Issue 2 / April 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 220-228
- Print publication:
- April 1989
-
- Article
-
- You have access
- Export citation
T-invariant algebras on Riemann surfaces
- Part of
-
- Journal:
- Mathematika / Volume 34 / Issue 2 / December 1987
- Published online by Cambridge University Press:
- 26 February 2010, pp. 160-171
- Print publication:
- December 1987
-
- Article
- Export citation
Characterisation theorems for compact hypercomplex manifolds
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 43 / Issue 2 / October 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 231-245
- Print publication:
- October 1987
-
- Article
-
- You have access
- Export citation
A gap condition for the zeroes of certain polynomials in Kaplan classes K(α, β)
- Part of
-
- Journal:
- Mathematika / Volume 34 / Issue 1 / June 1987
- Published online by Cambridge University Press:
- 26 February 2010, pp. 53-63
- Print publication:
- June 1987
-
- Article
- Export citation
Extremal problems for a class of functions of positive real part and applications
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 2 / October 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 152-164
- Print publication:
- October 1986
-
- Article
-
- You have access
- Export citation
A variational method for the construction of convergent iterative sequences
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 1 / August 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 51-58
- Print publication:
- August 1986
-
- Article
-
- You have access
- Export citation
Unique solvability of the strong Hamburger moment problem
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 40 / Issue 1 / February 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 5-19
- Print publication:
- February 1986
-
- Article
-
- You have access
- Export citation
On Hayman's alternative
- Part of
-
- Journal:
- Mathematika / Volume 32 / Issue 1 / June 1985
- Published online by Cambridge University Press:
- 26 February 2010, pp. 139-146
- Print publication:
- June 1985
-
- Article
- Export citation
Jakubowski starlike integral operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 1 / August 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 117-127
- Print publication:
- August 1984
-
- Article
-
- You have access
- Export citation
Simultaneous Iteration by Entire or Rational Functions and Their Inverses
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 34 / Issue 3 / June 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 364-367
- Print publication:
- June 1983
-
- Article
-
- You have access
- Export citation
Dirichlet-finite outer functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 3 / October 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 289-293
- Print publication:
- October 1981
-
- Article
-
- You have access
- Export citation
The transformation of concentric circles into concentric rectangles
- Part of
-
- Journal:
- Mathematika / Volume 28 / Issue 1 / June 1981
- Published online by Cambridge University Press:
- 26 February 2010, pp. 141-152
- Print publication:
- June 1981
-
- Article
- Export citation
An integral mean inequality for starlike functions
- Part of
-
- Journal:
- Mathematika / Volume 28 / Issue 1 / June 1981
- Published online by Cambridge University Press:
- 26 February 2010, pp. 88-98
- Print publication:
- June 1981
-
- Article
- Export citation
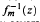 with an arbitrary initial point, where
with an arbitrary initial point, where 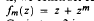 with m ≥ 2. We also show by several counterexamples that Rubinstein's Conjecture 2 is generally false.
with m ≥ 2. We also show by several counterexamples that Rubinstein's Conjecture 2 is generally false.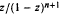 is starlike of order α 0 ≤ α < 1. We determine extreme points, inclusion relations, and show how this family acts under various linear operators.
is starlike of order α 0 ≤ α < 1. We determine extreme points, inclusion relations, and show how this family acts under various linear operators.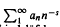 and their order (or Lindelöf) function μ(σ) (= inf{α;
and their order (or Lindelöf) function μ(σ) (= inf{α; with the solution of a previous problem of Bohr; (3) the following answer to the last problem: μ′(σ) can approach − ½, and necessarily μ(σ + μ(σ) + ½) = 0. The characterization of the order functions of ordinary Dirichlet series remains an open question.
with the solution of a previous problem of Bohr; (3) the following answer to the last problem: μ′(σ) can approach − ½, and necessarily μ(σ + μ(σ) + ½) = 0. The characterization of the order functions of ordinary Dirichlet series remains an open question.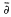 -equation. This, in turn, can be used, analogously to the Cauchy transform on the plane, to develop meromorphic (rational) approximation theory. We sketch the path of the development but omit most of the details when they are very much similar to the planar case. Our presentation follows closely that of [7]. The original motivation for this study was to obtain more information on Gleason parts useful in the study of Carleman (tangential) approximation theory (see [5]).
-equation. This, in turn, can be used, analogously to the Cauchy transform on the plane, to develop meromorphic (rational) approximation theory. We sketch the path of the development but omit most of the details when they are very much similar to the planar case. Our presentation follows closely that of [7]. The original motivation for this study was to obtain more information on Gleason parts useful in the study of Carleman (tangential) approximation theory (see [5]).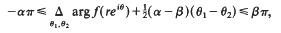
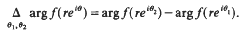
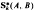 and the radius of convexity for
and the radius of convexity for 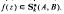 .
.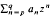 . By this means the authors and W. B. Jones (
. By this means the authors and W. B. Jones (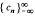 , to find a distribution function ψ(
, to find a distribution function ψ(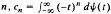 . In this article further menthods such as analogues of the Lioville-Ostrogradski formula and of the Christoffel-Darboux formula are developed to investigated When the moment porblem has a unique solution. This will be the case if and only if a sequence of nested disks associated with the sequence
. In this article further menthods such as analogues of the Lioville-Ostrogradski formula and of the Christoffel-Darboux formula are developed to investigated When the moment porblem has a unique solution. This will be the case if and only if a sequence of nested disks associated with the sequence 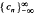 has only a point as its intersection (the so called limit point case).
has only a point as its intersection (the so called limit point case).
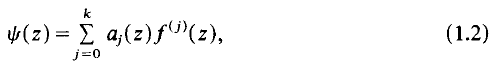
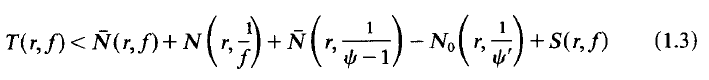
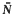
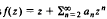 regular and satisfying │
regular and satisfying │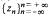 is established which has the properties
is established which has the properties 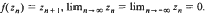 . The result certainly implies
. The result certainly implies 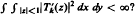 We shall show, among other results, that the answer is in the positive if
We shall show, among other results, that the answer is in the positive if 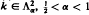 , with ess inf
, with ess inf