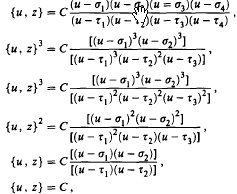Refine listing
Actions for selected content:
543 results in 30xxx
The locally convex topology on the space of meromorphic functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 3 / December 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 287-303
- Print publication:
- December 1995
-
- Article
-
- You have access
- Export citation
Multipliers of Cauchy integrals of logarithmic potentials
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 2 / December 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 397-405
- Print publication:
- December 1995
-
- Article
- Export citation
Some local properties of the solutions of second-order differential equations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 2 / October 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 255-265
- Print publication:
- October 1995
-
- Article
-
- You have access
- Export citation
Transient characteristics of an M/M/∞ system
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 862-888
- Print publication:
- September 1995
-
- Article
- Export citation
Normal families of holomorphic functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 1 / August 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 112-117
- Print publication:
- August 1995
-
- Article
-
- You have access
- Export citation
The parabolicity of Brelot's harmonic spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 1 / August 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 20-27
- Print publication:
- August 1995
-
- Article
-
- You have access
- Export citation
Hyperbolic linear invariance and hyperbolic k-convexity
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 1 / February 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 73-93
- Print publication:
- February 1995
-
- Article
-
- You have access
- Export citation
Inequalities and representation formulas for functions of exponential type
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 1 / February 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 15-26
- Print publication:
- February 1995
-
- Article
-
- You have access
- Export citation
Möbius covariance of iterated Dirac operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 3 / June 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 403-414
- Print publication:
- June 1994
-
- Article
-
- You have access
- Export citation
Complex length coordinates for quasi-fuchsian groups
- Part of
-
- Journal:
- Mathematika / Volume 41 / Issue 1 / June 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 173-188
- Print publication:
- June 1994
-
- Article
- Export citation
When is the composition of two power series even?
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 3 / June 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 415-420
- Print publication:
- June 1994
-
- Article
-
- You have access
- Export citation
Cusps, triangle groups and hyperbolic 3-folds
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 55 / Issue 2 / October 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 149-182
- Print publication:
- October 1993
-
- Article
-
- You have access
- Export citation
Two sharp inequalities for the norm of a factor of a polynomial
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 341-349
- Print publication:
- December 1992
-
- Article
- Export citation
Markov chains and generalized continued fractions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 838-849
- Print publication:
- December 1992
-
- Article
- Export citation
The strong c-Symmetric distribution
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 53 / Issue 2 / October 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 261-265
- Print publication:
- October 1992
-
- Article
-
- You have access
- Export citation
Euclidean linear invariance and uniform local convexity
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 52 / Issue 3 / June 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 401-418
- Print publication:
- June 1992
-
- Article
-
- You have access
- Export citation
The spectral theory of multiplication operators and the recurrence properties for nondifferentiable functions in the Zygmund class Λ*a
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 1 / June 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 136-151
- Print publication:
- June 1992
-
- Article
- Export citation
Limit points of partial sums of Taylor series
- Part of
-
- Journal:
- Mathematika / Volume 38 / Issue 2 / December 1991
- Published online by Cambridge University Press:
- 26 February 2010, pp. 239-249
- Print publication:
- December 1991
-
- Article
- Export citation
Star-center points of univalent functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 51 / Issue 1 / August 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 95-105
- Print publication:
- August 1991
-
- Article
-
- You have access
- Export citation
Admissible solutions of the Schwarzian differential equation
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 2 / April 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 258-278
- Print publication:
- April 1991
-
- Article
-
- You have access
- Export citation
 The concept of linear invariance has proved fruitful in geometric function theory. One aspect of Pommerenke's work is the extension of certain results from classical univalent function theory to linearly invariant functions. We propose a definition of a related concept that we call hyperbolic linear invariance for locally schlicht holomorphic functions that map the unit disk into itself. We obtain results for hyperbolic linearly invariant functions which generalize parts of the theory of bounded univalent functions. There are many similarities between linearly invariant functions and hyperbolic linearly invariant functions, but some new phenomena also arise in the study of hyperbolic linearly invariant functions.
The concept of linear invariance has proved fruitful in geometric function theory. One aspect of Pommerenke's work is the extension of certain results from classical univalent function theory to linearly invariant functions. We propose a definition of a related concept that we call hyperbolic linear invariance for locally schlicht holomorphic functions that map the unit disk into itself. We obtain results for hyperbolic linearly invariant functions which generalize parts of the theory of bounded univalent functions. There are many similarities between linearly invariant functions and hyperbolic linearly invariant functions, but some new phenomena also arise in the study of hyperbolic linearly invariant functions.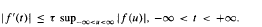 . Moreover we obtain a new representation formula for entire functions of exponential type.
. Moreover we obtain a new representation formula for entire functions of exponential type. and
and 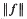 be the maximum of
be the maximum of 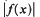 on the unit circle. We prove that
on the unit circle. We prove that 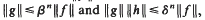 , where β =
, where β = 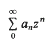
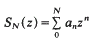
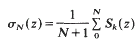
 be the class of normalized univalent functions in the unit disk. For
be the class of normalized univalent functions in the unit disk. For  where
where  is the interior of
is the interior of 
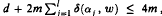 , where α
, where α