Refine listing
Actions for selected content:
543 results in 30xxx
ANALYTIC PROPERTIES OF MIRROR MAPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 22 November 2012, pp. 195-235
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
IRRATIONALITY AND NONQUADRATICITY MEASURES FOR LOGARITHMS OF ALGEBRAIC NUMBERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 22 November 2012, pp. 237-267
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
An argument of a function in H1/2
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 23 February 2012, pp. 507-511
-
- Article
-
- You have access
- Export citation
A non-Archimedean Montel’s theorem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 21 February 2012, pp. 966-990
- Print publication:
- May 2012
-
- Article
-
- You have access
- Export citation
UNIQUENESS OF MEROMORPHIC FUNCTIONS SHARING ONE VALUE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 04 January 2012, pp. 280-294
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
ON PROPERTIES OF FINITE-ORDER MEROMORPHIC SOLUTIONS OF A CERTAIN DIFFERENCE PAINLEVÉ I EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 08 December 2011, pp. 463-475
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
ON THE ALGEBRAIC CONVERGENCE OF FINITELY GENERATED KLEINIAN GROUPS IN ALL DIMENSIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 08 December 2011, pp. 275-279
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
UNIQUENESS OF ENTIRE FUNCTIONS SHARING A VALUE WITH LINEAR DIFFERENTIAL POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 30 November 2011, pp. 295-306
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
NORMAL FAMILIES OF ZERO-FREE MEROMORPHIC FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 91 / Issue 3 / December 2011
- Published online by Cambridge University Press:
- 16 November 2011, pp. 313-322
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
ESSENTIAL COMMUTATIVITY OF SOME INTEGRAL AND COMPOSITION OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 20 October 2011, pp. 143-153
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
Location of geodesics and isoperimetric inequalities in Denjoy domains
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 15 June 2011, pp. 245-269
-
- Article
-
- You have access
- Export citation
LANDAU’S THEOREM AND MARDEN CONSTANT FOR HARMONIC ν-BLOCH MAPPINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 1 / August 2011
- Published online by Cambridge University Press:
- 10 June 2011, pp. 19-32
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
ON HARMONIC BLOCH SPACES IN THE UNIT BALL OF ℂn
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 1 / August 2011
- Published online by Cambridge University Press:
- 10 June 2011, pp. 67-78
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
DIFFERENTIAL SUBORDINATIONS FOR CLASSES OF MEROMORPHIC p-VALENT FUNCTIONS DEFINED BY MULTIPLIER TRANSFORMATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 3 / June 2011
- Published online by Cambridge University Press:
- 05 April 2011, pp. 353-368
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
PROPERTY (FA) OF THE GAUSS–PICARD MODULAR GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 2 / October 2011
- Published online by Cambridge University Press:
- 15 March 2011, pp. 225-228
- Print publication:
- October 2011
-
- Article
-
- You have access
- Export citation
NEIGHBOURHOODS OF UNIVALENT FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 14 September 2010, pp. 210-219
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
LIMIT SETS AND COMMENSURABILITY OF KLEINIAN GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 1 / August 2010
- Published online by Cambridge University Press:
- 02 June 2010, pp. 1-9
- Print publication:
- August 2010
-
- Article
-
- You have access
- Export citation
NONDECREASING FUNCTIONS, EXCEPTIONAL SETS AND GENERALIZED BOREL LEMMAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 3 / June 2010
- Published online by Cambridge University Press:
- 11 June 2010, pp. 353-361
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
Ergodic properties of semi-hyperbolic functions with polynomial Schwarzian derivative
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 30 April 2010, pp. 471-502
-
- Article
-
- You have access
- Export citation
Sets of determination and kernels of certain associated operators
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 30 April 2010, pp. 503-510
-
- Article
-
- You have access
- Export citation
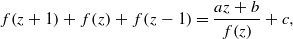
 . In this paper, we prove that if {
. In this paper, we prove that if {