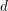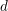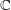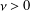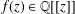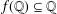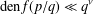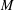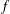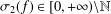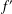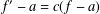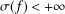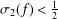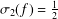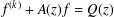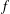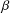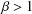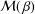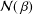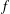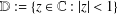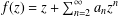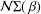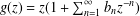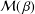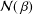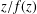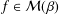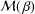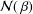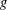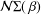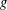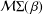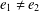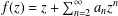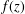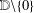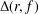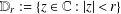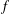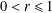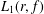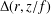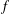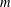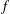Refine listing
Actions for selected content:
543 results in 30xxx
Mappings of Lp-integrable distortion: regularity of the inverse
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 16 May 2016, pp. 647-663
- Print publication:
- June 2016
-
- Article
- Export citation
A Convexity Property of Discrete Random Walks
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 6 / November 2016
- Published online by Cambridge University Press:
- 31 March 2016, pp. 928-940
-
- Article
- Export citation
ON THE EXISTENCE OF FINITE CRITICAL TRAJECTORIES IN A FAMILY OF QUADRATIC DIFFERENTIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 80-91
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
SEMIGROUPS OF COMPOSITION OPERATORS ON LOCAL DIRICHLET SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 144-154
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
A GENERALISATION OF THE CLUNIE–SHEIL-SMALL THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 17 February 2016, pp. 92-100
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
Hausdorff Dimension of Sets of Escaping Points and Escaping Parameters for Elliptic Functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 30 December 2015, pp. 671-690
-
- Article
- Export citation
Integral points of bounded degree on affine curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 26 November 2015, pp. 754-768
- Print publication:
- April 2016
-
- Article
- Export citation
A NOTE ON LACUNARY POWER SERIES WITH RATIONAL COEFFICIENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 11 November 2015, pp. 372-374
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
LOCALISATION OF LINEAR DIFFERENTIAL EQUATIONS IN THE UNIT DISC BY A CONFORMAL MAP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 15 October 2015, pp. 260-271
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
ON THE BRÜCK CONJECTURE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 02 October 2015, pp. 248-259
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
COEFFICIENT INEQUALITIES AND YAMASHITA’S CONJECTURE FOR SOME CLASSES OF ANALYTIC FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 29 September 2015, pp. 1-20
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
QUASICONFORMAL SOLUTIONS OF POISSON EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 19 August 2015, pp. 420-428
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
The Hele-Shaw flow and moduli of holomorphic discs
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 12 / December 2015
- Published online by Cambridge University Press:
- 18 August 2015, pp. 2301-2328
- Print publication:
- December 2015
-
- Article
- Export citation
ON UNICITY OF MEROMORPHIC SOLUTIONS TO DIFFERENCE EQUATIONS OF MALMQUIST TYPE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 05 August 2015, pp. 92-98
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
INTEGRAL MEANS AND DIRICHLET INTEGRAL FOR CERTAIN CLASSES OF ANALYTIC FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 16 July 2015, pp. 315-333
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
MODULI SPACES OF SURFACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 10 April 2015, pp. 168-170
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
ON THE ESCAPING SET OF MEROMORPHIC FUNCTIONS WITH DIRECT TRACTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 02 April 2015, pp. 68-76
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
The M-set of λ exp(z)/z has infinite area
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 217 / March 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 133-159
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
INFINITE PRODUCTS OF CYCLOTOMIC POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 26 February 2015, pp. 400-411
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
UNIQUENESS THEOREMS FOR DIRICHLET SERIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 12 February 2015, pp. 389-399
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
 be an open set in ℝ
be an open set in ℝ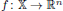 is a Sobolev homeomorphism. We study the regularity of
is a Sobolev homeomorphism. We study the regularity of 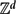
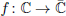 be a non-constant elliptic function. We prove that the Hausdorff dimension of the escaping set of
be a non-constant elliptic function. We prove that the Hausdorff dimension of the escaping set of