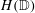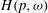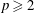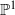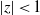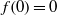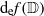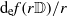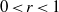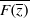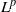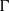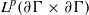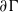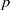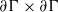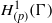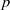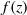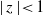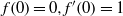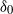Refine listing
Actions for selected content:
543 results in 30xxx
CHARACTERISATIONS OF HARDY GROWTH SPACES WITH DOUBLING WEIGHTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 12 May 2014, pp. 275-282
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
A PROBABILISTIC PROOF OF THE OPEN MAPPING THEOREM FOR ANALYTIC FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 17 December 2013, pp. 74-76
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
COEFFICIENT ESTIMATES, LANDAU’S THEOREM AND LIPSCHITZ-TYPE SPACES ON PLANAR HARMONIC MAPPINGS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 198-215
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
SPECIAL CURVES AND POSTCRITICALLY FINITE POLYNOMIALS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 1 / 2013
- Published online by Cambridge University Press:
- 19 September 2013, e3
-
- Article
-
- You have access
- Open access
- Export citation
REMARKS ON THE UNIVALENCE CRITERION OF PASCU AND PASCU
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 22 August 2013, pp. 210-216
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
DENSITY ESTIMATES ON COMPOSITE POLYNOMIALS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 07 August 2013, pp. 329-342
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
UNIQUENESS OF MEROMORPHIC FUNCTIONS WITH WEAKLY WEIGHTED SHARING
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 28 June 2013, pp. 26-43
- Print publication:
- August 2013
-
- Article
-
- You have access
- Export citation
HAMILTON SEQUENCES FOR EXTREMAL QUASICONFORMAL MAPPINGS OF DOUBLY-CONNECTED DOMAINS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 22 March 2013, pp. 376-379
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
EXTREME POINTS OF INTEGRAL FAMILIES OF ANALYTIC FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 14 March 2013, pp. 202-221
- Print publication:
- April 2013
-
- Article
-
- You have access
- Export citation
HOLOMORPHIC FUNCTIONS WITH IMAGE OF GIVEN LOGARITHMIC OR ELLIPTIC CAPACITY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 08 March 2013, pp. 145-157
- Print publication:
- April 2013
-
- Article
-
- You have access
- Export citation
Random Walks Reaching Against all Odds the other Side of the Quarter Plane
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 50 / Issue 1 / March 2013
- Published online by Cambridge University Press:
- 30 January 2018, pp. 85-102
- Print publication:
- March 2013
-
- Article
-
- You have access
- Export citation
De Branges’ theorem on approximation problems of Bernstein type
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 12 / Issue 4 / October 2013
- Published online by Cambridge University Press:
- 27 February 2013, pp. 879-899
- Print publication:
- October 2013
-
- Article
- Export citation
Proper isometric actions of hyperbolic groups on
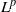 $L^p$-spaces
$L^p$-spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 5 / May 2013
- Published online by Cambridge University Press:
- 26 February 2013, pp. 773-792
- Print publication:
- May 2013
-
- Article
- Export citation
Generalized ‘second Ritt theorem’ and explicit solution of the polynomial moment problem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 4 / April 2013
- Published online by Cambridge University Press:
- 29 January 2013, pp. 705-728
- Print publication:
- April 2013
-
- Article
- Export citation
LIPSCHITZ SPACES AND BOUNDED MEAN OSCILLATION OF HARMONIC MAPPINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 18 January 2013, pp. 143-157
- Print publication:
- August 2013
-
- Article
-
- You have access
- Export citation
UNIVALENCE CRITERIA AND ANALOGUES OF THE JOHN CONSTANT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 12 December 2012, pp. 423-434
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
CONFORMAL SLIT MAPS IN APPLIED MATHEMATICS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 53 / Issue 3 / January 2012
- Published online by Cambridge University Press:
- 17 September 2012, pp. 171-189
-
- Article
-
- You have access
- Export citation
THE COMPLEXITY OF RIEMANN SURFACES AND THE HURWITZ EXISTENCE PROBLEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 02 August 2012, pp. 131-138
- Print publication:
- February 2013
-
- Article
-
- You have access
- Export citation
GENERATING SYSTEMS OF SUBGROUPS IN SU(2, 1)
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 07 June 2012, pp. 346-352
- Print publication:
- April 2013
-
- Article
-
- You have access
- Export citation
Cyclicity of singular inner functions from the corona theorem
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 11 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 31 May 2012, pp. 815-824
- Print publication:
- October 2012
-
- Article
- Export citation