Refine listing
Actions for selected content:
543 results in 30xxx
DISCRETE AND DENSE SUBGROUPS ACTING ON COMPLEX HYPERBOLIC SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 211-224
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
ON INFINITESIMAL TEICHMÜLLER SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 293-300
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
ON T DIRECTION OF ALGEBROID FUNCTION DEALING WITH MULTIPLE VALUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 147-156
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
The zeros of random polynomials cluster uniformly near the unit circle
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 3 / May 2008
- Published online by Cambridge University Press:
- 01 May 2008, pp. 734-746
- Print publication:
- May 2008
-
- Article
-
- You have access
- Export citation
A SECTORIAL THEOREM ON COMPLETELY RAMIFIED RATIONAL FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 131-138
- Print publication:
- February 2008
-
- Article
-
- You have access
- Export citation
A MODEL OF UNIVERSAL TEICHMÜLLER SPACE AND ITS APPLICATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 21-30
- Print publication:
- February 2008
-
- Article
-
- You have access
- Export citation
Permutable functions concerning differential equations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 3 / December 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 369-384
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
Quasiregular self-mappings of manifolds and word hyperbolic groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 6 / November 2007
- Published online by Cambridge University Press:
- 01 November 2007, pp. 1613-1622
- Print publication:
- November 2007
-
- Article
-
- You have access
- Export citation
Transcendental meromorphic solutions of some algebraic differential equations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 2 / October 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 157-180
- Print publication:
- October 2007
-
- Article
-
- You have access
- Export citation
Maximal convergence groups and rank one symmetric spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 1 / August 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-10
- Print publication:
- August 2007
-
- Article
-
- You have access
- Export citation
Derivative-free characterizations of Qk spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 2 / April 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 283-295
- Print publication:
- April 2007
-
- Article
-
- You have access
- Export citation
Radial distributions of Julia sets of meromorphic functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 3 / December 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 363-368
- Print publication:
- December 2006
-
- Article
-
- You have access
- Export citation
On Generalized Schwarz-Pick Estimates
- Part of
-
- Journal:
- Mathematika / Volume 53 / Issue 1 / June 2006
- Published online by Cambridge University Press:
- 21 December 2009, pp. 161-168
- Print publication:
- June 2006
-
- Article
- Export citation
Growth properties and sequences of zeros of analytic functions in spaces of Dirichlet type
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 3 / June 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 397-418
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
Omitted rays and wedges of fractional Cauchy transforms
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 3 / June 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 367-373
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
Topologies on spaces of vector-valued meromorphic functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 2 / April 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 273-290
- Print publication:
- April 2005
-
- Article
-
- You have access
- Export citation
Multiplicities in Hayman's alternative
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 1 / February 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 37-58
- Print publication:
- February 2005
-
- Article
-
- You have access
- Export citation
On the value distribution of f2f(k)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 1 / February 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 17-26
- Print publication:
- February 2005
-
- Article
-
- You have access
- Export citation
Further results on meromorphic functions that share two values with their derivatives
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 1 / February 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 91-102
- Print publication:
- February 2005
-
- Article
-
- You have access
- Export citation
U-Operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 1 / February 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 59-90
- Print publication:
- February 2005
-
- Article
-
- You have access
- Export citation
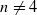 ), then every quasiregular mapping
), then every quasiregular mapping 
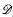
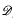
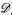
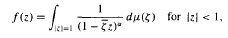 where μ is a complex-valued Borel measure on the unit circle. We show that if
where μ is a complex-valued Borel measure on the unit circle. We show that if 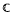 : |z| < 1} and there are two nonparallel rays in
: |z| < 1} and there are two nonparallel rays in 