Refine listing
Actions for selected content:
543 results in 30xxx
Analysis of generalized processor-sharing systems with two classes of customers and exponential services
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 832-858
- Print publication:
- September 2004
-
- Article
- Export citation
Normality and exceptional functions of derivatives
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 3 / June 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 403-414
- Print publication:
- June 2004
-
- Article
-
- You have access
- Export citation
A note on normality and shared values
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 1 / February 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 141-150
- Print publication:
- February 2004
-
- Article
-
- You have access
- Export citation
Smale's mean value conjecture for odd polynomials
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 3 / December 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 409-412
- Print publication:
- December 2003
-
- Article
-
- You have access
- Export citation
Unbounded analytic functions on plane domains
- Part of
-
- Journal:
- Mathematika / Volume 50 / Issue 1-2 / December 2003
- Published online by Cambridge University Press:
- 26 February 2010, pp. 207-214
- Print publication:
- December 2003
-
- Article
- Export citation
Lacunas in the Support of the Weyl Calculus for Two Hermitian Matrices
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 1 / August 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 85-124
- Print publication:
- August 2003
-
- Article
-
- You have access
- Export citation
Even and odd entire functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 1 / February 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 19-24
- Print publication:
- February 2003
-
- Article
-
- You have access
- Export citation
Parametrizing simple closed geodesy on Γ3\ℋ
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 1 / February 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 43-60
- Print publication:
- February 2003
-
- Article
-
- You have access
- Export citation
Extremal partitions and distortion under the Montel bounded univalent maps
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 3 / December 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 419-432
- Print publication:
- December 2002
-
- Article
-
- You have access
- Export citation
Strongly omnipresent operators: general conditions and applications to composition operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 3 / June 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 335-348
- Print publication:
- June 2002
-
- Article
-
- You have access
- Export citation
Calderón-type reproducing formulae on Lipschitz curves and surfaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 1 / February 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 33-46
- Print publication:
- February 2002
-
- Article
-
- You have access
- Export citation
The zeros of linear combinations of translates of polynomials
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 1 / February 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 109-118
- Print publication:
- February 2002
-
- Article
-
- You have access
- Export citation
About a problem of Hermite and Biehler
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 1 / February 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 87-92
- Print publication:
- February 2002
-
- Article
-
- You have access
- Export citation
On transcendental meromorphic functions which are geometrically finite
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 1 / February 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 93-108
- Print publication:
- February 2002
-
- Article
-
- You have access
- Export citation
Growth of functions in cercles de remplissage
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 1 / February 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 131-136
- Print publication:
- February 2002
-
- Article
-
- You have access
- Export citation
Arakelyan's theorem and relations between two harmonic functions
- Part of
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 February 2010, pp. 301-304
- Print publication:
- December 2001
-
- Article
- Export citation
On real forms of a complex algebraic curve
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 1 / February 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 134-142
- Print publication:
- February 2001
-
- Article
-
- You have access
- Export citation
Sharp starlikeness conditions for analytic functions with bounded derivative
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 3 / December 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 303-315
- Print publication:
- December 2000
-
- Article
-
- You have access
- Export citation
Weighted composition operators in weighted Banach spaces of analytic functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 1 / August 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 41-60
- Print publication:
- August 2000
-
- Article
-
- You have access
- Export citation
On families of Cauchy transforms and BMOA
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 68 / Issue 3 / June 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 357-364
- Print publication:
- June 2000
-
- Article
-
- You have access
- Export citation
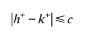
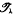 }, where
}, where 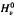 and
and 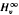 . we estimate the essential norm of a weighted composition operator and compute it for those Banach spaces
. we estimate the essential norm of a weighted composition operator and compute it for those Banach spaces 