Refine listing
Actions for selected content:
543 results in 30xxx
THE FILLING DISKS OF AN ALGEBROID FUNCTION IN THE UNIT DISK
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 3 / June 2010
- Published online by Cambridge University Press:
- 25 March 2010, pp. 455-464
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
SMALE’S PROBLEM FOR CRITICAL POINTS ON CERTAIN TWO RAYS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 25 March 2010, pp. 183-191
- Print publication:
- April 2010
-
- Article
-
- You have access
- Export citation
A NOTE ON VALUE DISTRIBUTION OF DIFFERENCE POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 3 / June 2010
- Published online by Cambridge University Press:
- 05 March 2010, pp. 353-360
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
UNIVALENT HARMONIC MAPPINGS INTO TWO-SLIT DOMAINS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 22 January 2010, pp. 61-73
- Print publication:
- February 2010
-
- Article
-
- You have access
- Export citation
Rate of growth of frequently hypercyclic functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 12 January 2010, pp. 39-59
-
- Article
-
- You have access
- Export citation
A CLUNIE LEMMA FOR DIFFERENCE AND q-DIFFERENCE POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 02 October 2009, pp. 23-32
- Print publication:
- February 2010
-
- Article
-
- You have access
- Export citation
JØRGENSEN’S INEQUALITY FOR QUATERNIONIC HYPERBOLIC SPACE WITH ELLIPTIC ELEMENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 02 October 2009, pp. 121-131
- Print publication:
- February 2010
-
- Article
-
- You have access
- Export citation
SINGULARITIES OF QUADRATIC DIFFERENTIALS AND EXTREMAL TEICHMÜLLER MAPPINGS DEFINED BY DEHN TWISTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 87 / Issue 2 / October 2009
- Published online by Cambridge University Press:
- 09 October 2009, pp. 275-288
- Print publication:
- October 2009
-
- Article
-
- You have access
- Export citation
Integer points of analytic functions in a half-plane
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 3 / October 2009
- Published online by Cambridge University Press:
- 23 September 2009, pp. 619-630
-
- Article
-
- You have access
- Export citation
Inner functions in the Möbius invariant Besov-type spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 3 / October 2009
- Published online by Cambridge University Press:
- 23 September 2009, pp. 751-770
-
- Article
-
- You have access
- Export citation
Riesz bases of reproducing kernels in Fock-type spaces
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 3 / July 2010
- Published online by Cambridge University Press:
- 23 July 2009, pp. 449-461
- Print publication:
- July 2010
-
- Article
- Export citation
NORMALITY AND SHARED SETS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 3 / June 2009
- Published online by Cambridge University Press:
- 01 June 2009, pp. 339-354
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
INVERSE IMAGES OF SECTORS BY FUNCTIONS IN WEIGHTED BERGMAN–ORLICZ SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 01 April 2009, pp. 233-247
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
Analytic functions associated with strong Hamburger moment problems
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 02 February 2009, pp. 181-187
-
- Article
-
- You have access
- Export citation
Holomorphic mappings between compact Riemann surfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 02 February 2009, pp. 109-126
-
- Article
-
- You have access
- Export citation
Meromorphic functions with shared limit values of positive linear measure
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 02 February 2009, pp. 235-240
-
- Article
-
- You have access
- Export citation
NEW CHARACTERIZATIONS OF THE MEROMORPHIC BESOV, Qp AND RELATED CLASSES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 09 February 2009, pp. 49-58
- Print publication:
- February 2009
-
- Article
-
- You have access
- Export citation
REGULARITY OF CURVES WITH A CONTINUOUS TANGENT LINE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 01 February 2009, pp. 17-26
- Print publication:
- February 2009
-
- Article
-
- You have access
- Export citation
CONSTRUCTING HERMAN RINGS BY TWISTING ANNULUS HOMEOMORPHISMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 01 February 2009, pp. 139-143
- Print publication:
- February 2009
-
- Article
-
- You have access
- Export citation
ON KLEINIAN GROUPS WITH THE SAME SET OF AXES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 437-441
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
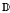 belongs to
belongs to 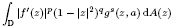
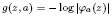 is the Green function of
is the Green function of 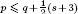 . Moreover, it is proved that, if 0<
. Moreover, it is proved that, if 0<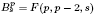 for some (equivalently for all)
for some (equivalently for all) 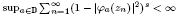 .
.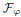 with radial weights ϕ we study the existence of Riesz bases of (normalized) reproducing kernels. We prove that these spaces possess such bases if and only if ϕ(
with radial weights ϕ we study the existence of Riesz bases of (normalized) reproducing kernels. We prove that these spaces possess such bases if and only if ϕ(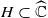 such that (1)
such that (1) 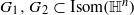 with the same set of axes are commensurable. We give some partial solutions.
with the same set of axes are commensurable. We give some partial solutions.