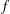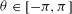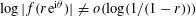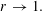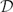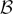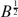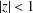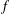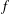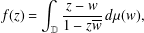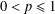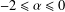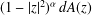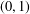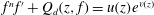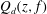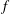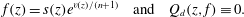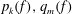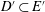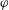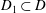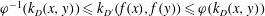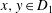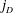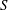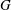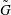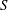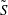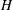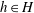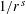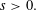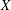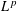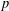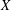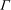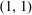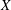Refine listing
Actions for selected content:
543 results in 30xxx
UNIVALENT FUNCTIONS AND RADIAL GROWTH
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 16 January 2015, pp. 531-546
- Print publication:
- September 2015
-
- Article
- Export citation
ON THE CONNECTEDNESS OF THE BRANCH LOCI OF NON-ORIENTABLE UNBORDERED KLEIN SURFACES OF LOW GENUS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 22 December 2014, pp. 211-230
- Print publication:
- January 2015
-
- Article
-
- You have access
- Export citation
GROWTH CONDITIONS FOR OPERATORS WITH SMALLEST SPECTRUM
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 18 December 2014, pp. 665-680
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
WEIGHTED COMPOSITION OPERATORS ON H∞ ∩
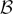 $\mathcal{B}$o
$\mathcal{B}$o
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 17 December 2014, pp. 475-480
- Print publication:
- May 2015
-
- Article
-
- You have access
- Export citation
ON THE COMPLEXITY OF FINDING A NECESSARY AND SUFFICIENT CONDITION FOR BLASCHKE-OSCILLATORY EQUATIONS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 17 December 2014, pp. 543-554
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
A VERSION OF ROUCHÉ’S THEOREM FOR CONTINUOUS FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 09 December 2014, pp. 268-272
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
CLASSIFICATION OF UNIVALENT HARMONIC MAPPINGS ON THE UNIT DISK WITH HALF-INTEGER COEFFICIENTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 12 November 2014, pp. 257-280
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
AN INTEGRAL REPRESENTATION FOR BESOV AND LIPSCHITZ SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 17 October 2014, pp. 129-144
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
LOGARITHMIC CONVEXITY OF AREA INTEGRAL MEANS FOR ANALYTIC FUNCTIONS II
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 14 October 2014, pp. 117-128
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
Products of twists, geodesic lengths and Thurston shears
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 2 / February 2015
- Published online by Cambridge University Press:
- 09 October 2014, pp. 313-350
- Print publication:
- February 2015
-
- Article
- Export citation
ON SOLUTIONS TO NONHOMOGENEOUS ALGEBRAIC DIFFERENTIAL EQUATIONS AND THEIR APPLICATION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 24 September 2014, pp. 391-403
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
FREELY QUASICONFORMAL MAPS AND DISTANCE RATIO METRIC
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 09 September 2014, pp. 383-390
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Numerical calculation of three-point branched covers of the projective line
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 September 2014, pp. 379-430
-
- Article
-
- You have access
- Export citation
Computing boundary extensions of conformal maps
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 September 2014, pp. 360-378
-
- Article
-
- You have access
- Export citation
REMARKS ON VALUE SHARING OF CERTAIN DIFFERENTIAL POLYNOMIALS OF MEROMORPHIC FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 28 August 2014, pp. 427-443
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Local rigidity for hyperbolic groups with Sierpiński carpet boundaries
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 11 / November 2014
- Published online by Cambridge University Press:
- 27 August 2014, pp. 1928-1938
- Print publication:
- November 2014
-
- Article
- Export citation
A VARIATION ON SELBERG’S APPROXIMATION PROBLEM
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 14 August 2014, pp. 213-235
- Print publication:
- January 2015
-
- Article
- Export citation
INVERSE BERNSTEIN INEQUALITIES AND MIN–MAX–MIN PROBLEMS ON THE UNIT CIRCLE
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 13 August 2014, pp. 581-590
- Print publication:
- September 2015
-
- Article
- Export citation
A GEOMETRIC STUDY OF WASSERSTEIN SPACES: ULTRAMETRICS
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 27 May 2014, pp. 162-178
- Print publication:
- January 2015
-
- Article
- Export citation
EXPLICIT BOUNDS ON AUTOMORPHIC AND CANONICAL GREEN FUNCTIONS OF FUCHSIAN GROUPS
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 2 / July 2014
- Published online by Cambridge University Press:
- 14 May 2014, pp. 257-306
- Print publication:
- July 2014
-
- Article
- Export citation