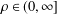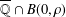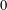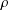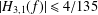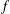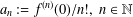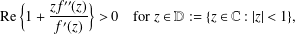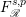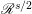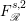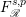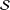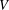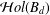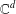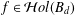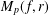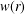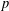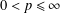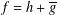Refine listing
Actions for selected content:
543 results in 30xxx
The Fréchet Schwartz Algebra of Uniformly Convergent Dirichlet Series
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 07 May 2018, pp. 933-942
-
- Article
- Export citation
A NOTE ON A COMPLETE SOLUTION OF A PROBLEM POSED BY K. MAHLER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 03 May 2018, pp. 60-63
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
On the existence of harmonic mappings between doubly connected domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 22 April 2018, pp. 619-628
- Print publication:
- June 2018
-
- Article
- Export citation
THE SHARP BOUND FOR THE HANKEL DETERMINANT OF THE THIRD KIND FOR CONVEX FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 04 April 2018, pp. 435-445
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
FRACTIONAL FOCK–SOBOLEV SPACES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 237 / March 2020
- Published online by Cambridge University Press:
- 06 March 2018, pp. 79-97
- Print publication:
- March 2020
-
- Article
-
- You have access
- HTML
- Export citation
TOEPLITZ DETERMINANTS WHOSE ELEMENTS ARE THE COEFFICIENTS OF ANALYTIC AND UNIVALENT FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 26 February 2018, pp. 253-264
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
Cluster algebras and continued fractions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 3 / March 2018
- Published online by Cambridge University Press:
- 22 December 2017, pp. 565-593
- Print publication:
- March 2018
-
- Article
- Export citation
UNIQUENESS THEOREMS FOR MAPPINGS OF FINITE DISTORTION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 07 November 2017, pp. 412-429
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
Applications of differential subordinations for norm estimates of an integral operator
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 06 November 2017, pp. 281-291
- Print publication:
- April 2018
-
- Article
- Export citation
NORM OF THE HILBERT MATRIX OPERATOR ON THE WEIGHTED BERGMAN SPACES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 18 October 2017, pp. 513-525
- Print publication:
- September 2018
-
- Article
-
- You have access
- Export citation
AN ENTIRE FUNCTION SHARING TWO VALUES WITH ITS LINEAR DIFFERENTIAL POLYNOMIAL
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 04 October 2017, pp. 265-273
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
LANDAU’S THEOREM FOR SOLUTIONS OF THE
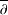 $\overline{\unicode[STIX]{x2202}}$ -EQUATION IN DIRICHLET-TYPE SPACES
$\overline{\unicode[STIX]{x2202}}$ -EQUATION IN DIRICHLET-TYPE SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 28 September 2017, pp. 80-87
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
Absolute continuity of distributions of one-dimensional Lévy processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 15 September 2017, pp. 852-872
- Print publication:
- September 2017
-
- Article
- Export citation
MAPPING PROPERTIES OF A SCALE INVARIANT CASSINIAN METRIC AND A GROMOV HYPERBOLIC METRIC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 18 August 2017, pp. 141-152
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
A SCHWARZ LEMMA FOR
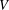 $V$ -HARMONIC MAPS AND THEIR APPLICATIONS
$V$ -HARMONIC MAPS AND THEIR APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 17 August 2017, pp. 504-512
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
INTEGRAL MEANS OF HOLOMORPHIC FUNCTIONS AS GENERIC LOG-CONVEX WEIGHTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 07 August 2017, pp. 88-93
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
ON CONVEX COMBINATIONS OF CONVEX HARMONIC MAPPINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 07 August 2017, pp. 256-262
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
From Hankel Operators to Carleson Measures in a Quaternionic Variable
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 17 July 2017, pp. 565-585
-
- Article
- Export citation
A Hybrid Spectral Element Method for Fractional Two-Point Boundary Value Problems
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 09 May 2017, pp. 437-464
- Print publication:
- May 2017
-
- Article
- Export citation
ON MULTIPLIERS BETWEEN SOME SPACES OF HOLOMORPHIC FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 29 March 2017, pp. 146-153
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation