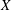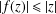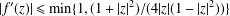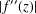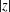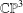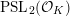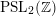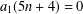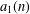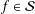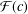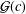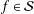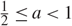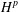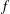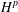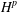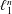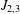Refine listing
Actions for selected content:
543 results in 30xxx
Green Function and Self-adjoint Laplacians on Polyhedral Surfaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 02 July 2019, pp. 1324-1351
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
ESTIMATES OF THE SECOND DERIVATIVE OF BOUNDED ANALYTIC FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 03 June 2019, pp. 458-469
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
ALGEBRAIC SURFACES WITH INFINITELY MANY TWISTOR LINES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 24 May 2019, pp. 61-70
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
Local-global principles in circle packings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 6 / June 2019
- Published online by Cambridge University Press:
- 20 May 2019, pp. 1118-1170
- Print publication:
- June 2019
-
- Article
- Export citation
Universal Entire Functions That Define Order Isomorphisms of Countable Real Sets
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 10 April 2019, pp. 767-779
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
VANISHING COEFFICIENTS IN FOUR QUOTIENTS OF INFINITE PRODUCT EXPANSIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 20 March 2019, pp. 216-224
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
GAUSSIAN CURVATURE AND UNICITY PROBLEM OF GAUSS MAPS OF VARIOUS CLASSES OF SURFACES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 240 / December 2020
- Published online by Cambridge University Press:
- 18 March 2019, pp. 275-297
- Print publication:
- December 2020
-
- Article
- Export citation
Division algebras of slice functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 15 March 2019, pp. 2055-2082
- Print publication:
- August 2020
-
- Article
- Export citation
LOGARITHMIC COEFFICIENTS PROBLEMS IN FAMILIES RELATED TO STARLIKE AND CONVEX FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 11 March 2019, pp. 230-249
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
From Steklov to Neumann and Beyond, via Robin: The Szegő Way
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 07 March 2019, pp. 1024-1043
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Is the Sibuya distribution a progeny?
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 12 July 2019, pp. 52-56
- Print publication:
- March 2019
-
- Article
- Export citation
COMPACT WEIGHTED COMPOSITION OPERATORS ON
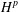 $H^{p}$-SPACES
$H^{p}$-SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 26 February 2019, pp. 473-484
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Lipschitz-free Spaces on Finite Metric Spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 13 February 2019, pp. 774-804
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
NOTE ON THE CONVOLUTION OF HARMONIC MAPPINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 13 February 2019, pp. 421-431
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
ON ODD-DIMENSIONAL COMPLEX ANALYTIC KLEINIAN GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 12 February 2019, pp. 1-32
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
Persistent Hall rays for Lagrange spectra at cusps of Riemann surfaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 11 February 2019, pp. 2017-2072
- Print publication:
- August 2020
-
- Article
- Export citation
A NOTE ON THE PERIODICITY OF ENTIRE FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 07 February 2019, pp. 290-296
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
SHARP BOUNDS OF SOME COEFFICIENT FUNCTIONALS OVER THE CLASS OF FUNCTIONS CONVEX IN THE DIRECTION OF THE IMAGINARY AXIS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 29 January 2019, pp. 86-96
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
Estimates for the order of Nevanlinna matrices and a Berezanskii-type theorem
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 26 January 2019, pp. 1637-1661
- Print publication:
- December 2019
-
- Article
- Export citation
Fatou components and singularities of meromorphic functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 23 January 2019, pp. 633-654
- Print publication:
- April 2020
-
- Article
- Export citation