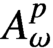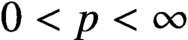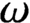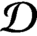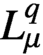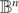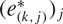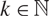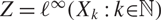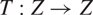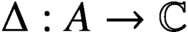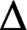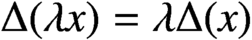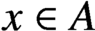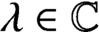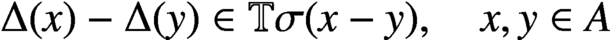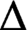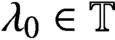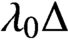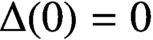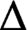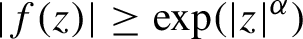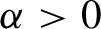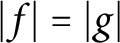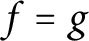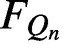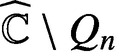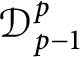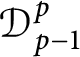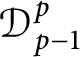Refine listing
Actions for selected content:
543 results in 30xxx
A VARIANT OF CAUCHY’S ARGUMENT PRINCIPLE FOR ANALYTIC FUNCTIONS WHICH APPLIES TO CURVES CONTAINING ZEROS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 18 January 2021, pp. 486-492
- Print publication:
- June 2021
-
- Article
- Export citation
GENERALISED WEIGHTED COMPOSITION OPERATORS ON BERGMAN SPACES INDUCED BY DOUBLING WEIGHTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 08 January 2021, pp. 141-153
- Print publication:
- August 2021
-
- Article
- Export citation
Bohr phenomenon for operator-valued functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 08 January 2021, pp. 72-86
-
- Article
- Export citation
Mixing operators with prescribed unimodular eigenvalues
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 28 December 2020, pp. 1-8
- Print publication:
- January 2022
-
- Article
- Export citation
Quasiconformality and hyperbolic skew
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 3 / November 2021
- Published online by Cambridge University Press:
- 18 December 2020, pp. 449-466
- Print publication:
- November 2021
-
- Article
- Export citation
CORRIGENDUM TO THE PAPER D. KALAJ, ON KELLOGG’S THEOREM FOR QUASICONFORMAL MAPPINGS. GLASG. MATH. J. 54, NO. 3, 599–603 (2012)
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 18 December 2020, p. 252
- Print publication:
- January 2022
-
- Article
-
- You have access
- Export citation
The factorisation property of l∞(Xk)
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 2 / September 2021
- Published online by Cambridge University Press:
- 10 December 2020, pp. 421-448
- Print publication:
- September 2021
-
- Article
-
- You have access
- Open access
- Export citation
A SPHERICAL VERSION OF THE KOWALSKI–SŁODKOWSKI THEOREM AND ITS APPLICATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 03 December 2020, pp. 386-411
- Print publication:
- December 2021
-
- Article
- Export citation
On the decay of singular inner functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 02 December 2020, pp. 902-905
- Print publication:
- December 2021
-
- Article
- Export citation
Exponential polynomials with Fatou and non-escaping sets of finite Lebesgue measure
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 20 November 2020, pp. 3821-3840
- Print publication:
- December 2021
-
- Article
-
- You have access
- Open access
- Export citation
Surjective isometries of metric geometries
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 28 October 2020, pp. 828-839
- Print publication:
- December 2021
-
- Article
- Export citation
Limits of geodesic push-forwards of horocycle invariant measures
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 23 October 2020, pp. 2782-2804
- Print publication:
- September 2021
-
- Article
- Export citation
Bohr theorems for slice regular functions over octonions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 21 October 2020, pp. 1595-1610
- Print publication:
- October 2021
-
- Article
- Export citation
A note on the phase retrieval of holomorphic functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 08 October 2020, pp. 779-786
- Print publication:
- December 2021
-
- Article
- Export citation
STARLIKENESS AND CONVEXITY OF CAUCHY TRANSFORMS ON REGULAR POLYGONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 05 October 2020, pp. 291-302
- Print publication:
- April 2021
-
- Article
- Export citation
INTEGRAL MEANS OF UNIVALENT FUNCTIONS ON AN ANNULUS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 21 September 2020, p. 512
- Print publication:
- June 2021
-
- Article
-
- You have access
- Export citation
Embedding of Dirichlet type spaces
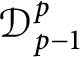 $\mathcal {D}^{p}_{p-1 }$ into tent spaces and Volterra operators
$\mathcal {D}^{p}_{p-1 }$ into tent spaces and Volterra operators
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 08 September 2020, pp. 697-708
- Print publication:
- September 2021
-
- Article
- Export citation
On the number of linearly independent admissible solutions to linear differential and linear difference equations
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 30 July 2020, pp. 1556-1591
- Print publication:
- December 2021
-
- Article
- Export citation
Continuity of condenser capacity under holomorphic motions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 29 June 2020, pp. 340-348
- Print publication:
- June 2021
-
- Article
- Export citation
Entropy in uniformly quasiregular dynamics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 22 June 2020, pp. 2397-2427
- Print publication:
- August 2021
-
- Article
- Export citation