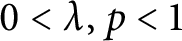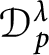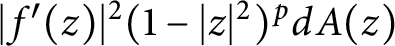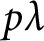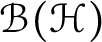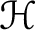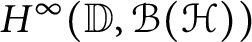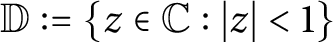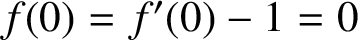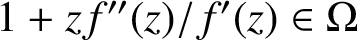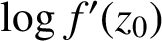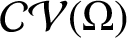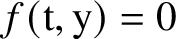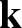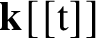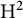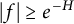Refine listing
Actions for selected content:
543 results in 30xxx
Circle packings, kissing reflection groups and critically fixed anti-rational maps
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 17 January 2022, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Corona and Wolff theorems for the multiplier algebra of Dirichlet–Morrey spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 13 January 2022, pp. 963-975
- Print publication:
- December 2022
-
- Article
- Export citation
Operator valued analogues of multidimensional Bohr’s inequality
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 10 January 2022, pp. 1020-1035
- Print publication:
- December 2022
-
- Article
- Export citation
Non-normality, topological transitivity and expanding families
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 3 / November 2022
- Published online by Cambridge University Press:
- 14 December 2021, pp. 511-523
- Print publication:
- November 2022
-
- Article
- Export citation
AN APPLICATION OF SCHUR’S ALGORITHM TO VARIABILITY REGIONS OF CERTAIN ANALYTIC FUNCTIONS II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 02 December 2021, pp. 468-481
- Print publication:
- June 2022
-
- Article
- Export citation
Abelian actions on compact nonorientable Riemann surfaces
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 02 December 2021, pp. 634-648
- Print publication:
- September 2022
-
- Article
- Export citation
Arquile Varieties – Varieties Consisting of Power Series in a Single Variable
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 01 December 2021, e78
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A criterion for normality of analytic mappings
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 19 November 2021, pp. 80-88
-
- Article
- Export citation
On unavoidable families of meromorphic functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 18 November 2021, pp. 114-123
- Print publication:
- March 2023
-
- Article
- Export citation
Typical properties of periodic Teichmüller geodesics: Lyapunov exponents
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 17 November 2021, pp. 556-584
- Print publication:
- February 2023
-
- Article
- Export citation
Julia sets of Zorich maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 15 November 2021, pp. 692-728
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Twisted cohomological equations for translation flows
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 22 October 2021, pp. 881-916
- Print publication:
- March 2022
-
- Article
- Export citation
Slices of parameter space for meromorphic maps with two asymptotic values
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 18 October 2021, pp. 99-139
- Print publication:
- January 2023
-
- Article
- Export citation
Weakly separated Bessel systems of model spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 04 October 2021, pp. 723-742
- Print publication:
- September 2022
-
- Article
- Export citation
FUNCTIONAL CALCULI FOR SECTORIAL OPERATORS AND RELATED FUNCTION THEORY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 04 October 2021, pp. 1383-1463
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SECOND HANKEL DETERMINANT OF LOGARITHMIC COEFFICIENTS OF CONVEX AND STARLIKE FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 30 September 2021, pp. 458-467
- Print publication:
- June 2022
-
- Article
- Export citation
A REVIEW OF ONE-PHASE HELE-SHAW FLOWS AND A LEVEL-SET METHOD FOR NONSTANDARD CONFIGURATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 63 / Issue 3 / July 2021
- Published online by Cambridge University Press:
- 23 September 2021, pp. 269-307
-
- Article
- Export citation
Invertibility Threshold for Nevanlinna Quotient Algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 10 September 2021, pp. 225-244
- Print publication:
- February 2023
-
- Article
- Export citation
HEDGEHOGS IN LEHMER’S PROBLEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 07 September 2021, pp. 236-242
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic first boundary value problem for elliptic operators
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 16 July 2021, pp. 571-581
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation