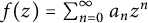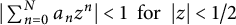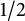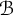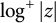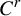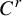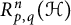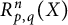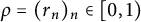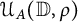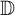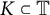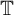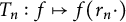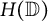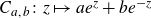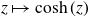Refine listing
Actions for selected content:
543 results in 30xxx
Bohr–Rogosinski radius for a certain class of close-to-convex harmonic mappings
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 31 January 2023, pp. 1014-1029
- Print publication:
- September 2023
-
- Article
- Export citation
Constructions of some families of smooth Cauchy transforms
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 26 January 2023, pp. 319-344
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mahler measure of polynomial iterates
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 12 January 2023, pp. 881-885
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Geometric filling curves on punctured surfaces
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 15 December 2022, pp. 383-400
- Print publication:
- May 2023
-
- Article
- Export citation
Asymptotically holomorphic methods for infinitely renormalizable
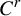 $C^r$ unimodal maps
$C^r$ unimodal maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 11 / November 2023
- Published online by Cambridge University Press:
- 29 November 2022, pp. 3636-3684
- Print publication:
- November 2023
-
- Article
- Export citation
Cyclic inner functions in growth classes and applications to approximation problems
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 23 November 2022, pp. 749-760
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Iterates of meromorphic functions on escaping Fatou components
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 22 November 2022, pp. 1906-1928
- Print publication:
- December 2023
-
- Article
- Export citation
The fundamental inequality for cocompact Fuchsian groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 21 November 2022, e102
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Estimates for generalized Bohr radii in one and higher dimensions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 04 November 2022, pp. 682-699
- Print publication:
- June 2023
-
- Article
- Export citation
Abel universal functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 26 October 2022, pp. 1957-1985
- Print publication:
- December 2023
-
- Article
- Export citation
Some remarks on approximation in several complex variables
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 17 October 2022, pp. 643-653
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Polynomial null solutions to bosonic Laplacians, bosonic Bergman and Hardy spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 4 / November 2022
- Published online by Cambridge University Press:
- 13 October 2022, pp. 958-989
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Geometric versions of Schwarz’s lemma for spherically convex functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 03 October 2022, pp. 1780-1799
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Topological dynamics of cosine maps
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 23 September 2022, pp. 497-529
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An algebraic approach to a quartic analogue of the Kontsevich model
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 20 September 2022, pp. 471-495
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SINGULAR DIRECTIONS IN VEECH SURFACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 16 September 2022, pp. 390-397
- Print publication:
- June 2023
-
- Article
- Export citation
A NOTE ON AN ASYMPTOTIC VERSION OF A PROBLEM OF MAHLER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 15 September 2022, pp. 398-402
- Print publication:
- June 2023
-
- Article
- Export citation
HANKEL MEASURES FOR FOCK SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 15 September 2022, pp. 290-295
- Print publication:
- April 2023
-
- Article
- Export citation
Zero and uniqueness sets for Fock spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 25 July 2022, pp. 532-543
- Print publication:
- June 2023
-
- Article
- Export citation
Profiling ponded soil surface in saturated seepage into drain-line sink: Kalashnikov’s method of lateral leaching revisited
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 12 July 2022, pp. 367-384
-
- Article
-
- You have access
- Open access
- HTML
- Export citation