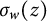Refine listing
Actions for selected content:
543 results in 30xxx
Solid bases and functorial constructions for (p-)Banach spaces of analytic functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 4 / November 2024
- Published online by Cambridge University Press:
- 09 September 2024, pp. 1013-1044
-
- Article
- Export citation
NOTES ON FERMAT-TYPE DIFFERENCE EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 03 June 2024, pp. 324-335
- Print publication:
- April 2025
-
- Article
- Export citation
Différentielles quadratiques à singularités prescrites
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 28 May 2024, pp. 1762-1826
- Print publication:
- October 2025
-
- Article
- Export citation
A classification of automorphic Lie algebras on complex tori
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 28 May 2024, pp. 947-989
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A TROPICAL ANALOGUE OF THE LEMMA ON THE LOGARITHMIC DERIVATIVE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 20 May 2024, pp. 303-312
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Phase retrieval on circles and lines
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 10 May 2024, pp. 927-935
- Print publication:
- December 2024
-
- Article
- Export citation
On Harnack inequality and harmonic Schwarz lemma
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 10 May 2024, pp. 940-954
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Growth of hypercyclic functions: a continuous path between
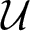 $\mathcal{U}$-frequent hypercyclicity and hypercyclicity
$\mathcal{U}$-frequent hypercyclicity and hypercyclicity
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 08 May 2024, pp. 794-829
-
- Article
- Export citation
Inhomogeneous Poisson processes in the disk and interpolation
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 30 April 2024, pp. 749-777
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Random analytic functions with a prescribed growth rate in the unit disk
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 26 April 2024, pp. 1546-1569
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SECOND HANKEL DETERMINANT FOR LOGARITHMIC INVERSE COEFFICIENTS OF CONVEX AND STARLIKE FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 18 April 2024, pp. 128-139
- Print publication:
- February 2025
-
- Article
- Export citation
Lower Bounds for the Canonical Height of a Unicritical Polynomial and Capacity
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 02 April 2024, e45
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the ergodic theory of the real Rel foliation
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 02 April 2024, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sobolev trace-type inequalities via time-space fractional heat equations
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 25 March 2024, pp. 1093-1134
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic expansions relating to the distribution of the length of longest increasing subsequences
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 15 March 2024, e36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A CLASS OF SYMBOLS THAT INDUCE BOUNDED COMPOSITION OPERATORS FOR DIRICHLET-TYPE SPACES ON THE DISC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 14 March 2024, pp. 140-145
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spectral theory of the invariant Laplacian on the disk and the sphere – a complex analysis approach
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 01 March 2024, pp. 940-974
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hausdorff operators on some classical spaces of analytic functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 29 February 2024, pp. 768-780
- Print publication:
- September 2024
-
- Article
- Export citation
ON THE ITERATIONS AND THE ARGUMENT DISTRIBUTION OF MEROMORPHIC FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 15 February 2024, pp. 145-170
- Print publication:
- April 2024
-
- Article
- Export citation
The Schwarzian norm estimates for Janowski convex functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 12 February 2024, pp. 299-315
-
- Article
- Export citation
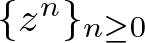
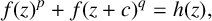
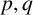
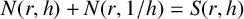
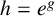

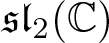
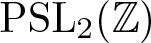



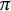

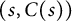
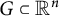
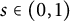
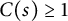
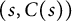

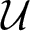








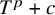
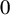
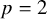
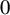
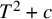
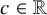
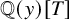
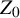
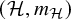
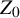
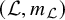
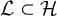
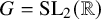
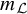
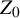
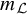






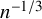

 of the “complexified unit circle”
of the “complexified unit circle”