We show the existence of transcendental entire functions $f: \mathbb {C} \rightarrow \mathbb {C}$ with Hausdorff-dimension $1$ Julia sets, such that every Fatou component of f has infinite inner connectivity. We also show that there exist singleton complementary components of any Fatou component of f, answering a question of Rippon and Stallard [Eremenko points and the structure of the escaping set. Trans. Amer. Math. Soc. 372(5) (2019), 3083–3111]. Our proof relies on a quasiconformal-surgery approach developed by Burkart and Lazebnik [Interpolation of power mappings. Rev. Mat. Iberoam. 39(3) (2023), 1181–1200].

In this article, by the use of nth derivative characterization, we obtain several some sufficient conditions for all solutions of the complex linear differential equation

$$ \begin{align*}f^{(n)}+A_{n-1}(z)f^{(n-1)}+\ldots+A_1(z)f'+A_0(z)f=A_n(z) \end{align*} $$

$A_i(z) (i=0,1,\ldots ,n)$

We introduce a relaxed version of the metric definition of quasiconformality that is natural also for mappings of low regularity, including $W_{\mathrm{loc}}^{1,1}({\mathbb R}^n;{\mathbb R}^n)$-mappings. Then we show on the plane that this relaxed definition can be used to prove Sobolev regularity, and that these ‘finely quasiconformal’ mappings are in fact quasiconformal.

In this note, it is shown that the differential polynomial of the form $Q(f)^{(k)}-p$ has infinitely many zeros and particularly $Q(f)^{(k)}$ has infinitely many fixed points for any positive integer k, where f is a transcendental meromorphic function, p is a nonzero polynomial and Q is a polynomial with coefficients in the field of small functions of f. The results are traced back to Problems 1.19 and 1.20 in the book of research problems by Hayman and Lingham [Research Problems in Function Theory, Springer, 2019]. As a consequence, we give an affirmative answer to an extended problem on the zero distribution of $(f^n)'-p$, proposed by Chiang and considered by Bergweiler [Bull. Hong Kong Math. Soc. 1(1997), p. 97–101].

In this article, we study the action of the the Hilbert matrix operator $H$ from the space of bounded analytic functions into conformally invariant Banach spaces. In particular, we describe the norm of $H$ from $H^\infty $ into $\text {BMOA}$ and we characterize the positive Borel measures $\mu $ such that $H$ is bounded from $H^\infty $ into the conformally invariant Dirichlet space $M(D_\mu )$. For particular measures $\mu $, we also provide the norm of $H$ from $H^\infty $ into $M(D_\mu )$.

Let µ be a finite positive Borelmeasure on $[0,1)$ and $\alpha \gt -1$. The generalized integral operator of Hilbert type $\mathcal {I}_{\mu_{\alpha+1}}$ is defined on the spaces $H(\mathbb{D})$ of analytic functions in the unit disc $\mathbb{D}$ as follows:

\begin{equation*}\mathcal {I}_{\mu_{\alpha+1}}(f)(z)=\int_{0}^{1} \frac{f(t)}{(1-tz)^{\alpha+1}}d\mu(t),\ \ f\in H(\mathbb{D}),\ \ z\in \mathbb{D} .\end{equation*}

In this paper, we give a unified characterization of the measures µ for which the operator $\mathcal {I}_{\mu_{\alpha+1}}$ is bounded from the Bloch space to a Bergman space for all $\alpha \gt -1$. Additionally, we also investigate the action of $\mathcal {I}_{\mu_{\alpha+1}}$ from the Bloch space to the Hardy spaces and the Besov spaces.

In this paper, we will show the Carleson measure characterizations for the boundedness and compactness of the Cesàro-type operator

\begin{equation*}\mathcal{C}_{\mu}(f)(z)=\sum^{\infty}_{n=0}\left( \int_{[0,1)}t^nd\mu(t)\right) \left(\sum^{n}_{k=0}a_k \right)z^n, \quad z\in \mathbb{D},\end{equation*}

acting on a number of important analytic function spaces on $\mathbb{D}$, where µ is a positive finite Borel measure. The function spaces are some newly appeared analytic function spaces (e.g., Bergman–Morrey spaces $A^{p,\lambda}$ and Dirichlet–Morrey spaces $\mathcal{D}_p^{\lambda}$) . This work continues the lines of the previous characterizations by Blasco and Galanopoulos et al. for classical Hardy spaces and weighted Bergman spaces and so forth.

We present a one-parameter family Fλ of transcendental entire functions with zeros, whose Newton’s method yields wandering domains, coexisting with the basins of the roots of Fλ. Wandering domains for Newton maps of zero-free functions have been built before by, e.g. Buff and Rückert [23] based on the lifting method. This procedure is suited to our Newton maps as members of the class of projectable functions (or maps of the cylinder), i.e. transcendental meromorphic functions f(z) in the complex plane that are semiconjugate, via the exponential, to some map g(w), which may have at most a countable number of essential singularities. In this paper, we make a systematic study of the general relation (dynamical and otherwise) between f and g, and inspect the extension of the logarithmic lifting method of periodic Fatou components to our context, especially for those g of finite-type. We apply these results to characterize the entire functions with zeros whose Newton’s method projects to some map g which is defined at both 0 and $\infty$. The family Fλ is the simplest in this class, and its parameter space shows open sets of λ-values in which the Newton map exhibits wandering or Baker domains, in both cases regions of initial conditions where Newton’s root-findingmethod fails.

We consider uniqueness problems for meromorphic inner functions on the upper half-plane. In these problems, we consider spectral data depending partially or fully on the spectrum, derivative values at the spectrum, Clark measure, or the spectrum of the negative of a meromorphic inner function. Moreover, we consider applications of these uniqueness results to inverse spectral theory of canonical Hamiltonian systems and obtain generalizations of the Borg-Levinson two-spectra theorem for canonical Hamiltonian systems and unique determination of a Hamiltonian from its spectral measure under some conditions.

In this paper, we establish a second main theorem for holomorphic maps with finite growth index on complex discs intersecting arbitrary families of hypersurfaces (fixed and moving) in projective varieties, which gives an above bound of the sum of truncated defects. Our result also generalizes and improves many previous second main theorems for holomorphic maps from ${\mathbb{C}}$ intersecting hypersurfaces (moving and fixed) in projective varieties.

For $r\in(0,1)$, let $\mu \left( r\right) $ be the modulus of the plane Grötzsch ring $\mathbb{B}^2\setminus[0,r]$, where $\mathbb{B}^2$ is the unit disk. In this paper, we prove that

\begin{equation*}\mu \left( r\right) =\ln \frac{4}{r}-\sum_{n=1}^{\infty }\frac{\theta _{n}}{2n}r^{2n},\end{equation*}

with $\theta _{n}\in \left( 0,1\right)$. Employing this series expansion, we obtain several absolutely monotonic and (logarithmically) completely monotonic functions involving $\mu \left( r\right) $, which yields some new results and extend certain known ones. Moreover, we give an affirmative answer to the conjecture proposed by Alzer and Richards in H. Alzer and K. Richards, On the modulus of the Grötzsch ring, J. Math. Anal. Appl. 432(1): (2015), 134–141, DOI 10.1016/j.jmaa.2015.06.057. As applications, several new sharp bounds and functional inequalities for $\mu \left( r\right) $ are established.

We study Toeplitz operators on the space of all real analytic functions on the real line and the space of all holomorphic functions on finitely connected domains in the complex plane. In both cases, we show that the space of all Toeplitz operators is isomorphic, when equipped with the topology of uniform convergence on bounded sets, with the symbol algebra. This is surprising in view of our previous results, since we showed that the symbol map is not continuous in this topology on the algebra generated by all Toeplitz operators. We also show that in the case of the Fréchet space of all holomorphic functions on a finitely connected domain in the complex plane, the commutator ideal is dense in the algebra generated by all Toeplitz operators in the topology of uniform convergence on bounded sets.

The sharp bound of the second Hankel determinant of logarithmic coefficients of inverse functions of strongly starlike functions is computed.

Let $\mathcal {S}$ denote the class of univalent functions in the open unit disc $\mathbb {D}:=\{z\in \mathbb {C}:\, |z|<1\}$ with the form $f(z)= z+\sum _{n=2}^{\infty }a_n z^n$. The logarithmic coefficients $\gamma _{n}$ of $f\in \mathcal {S}$ are defined by $F_{f}(z):= \log (f(z)/z)=2\sum _{n=1}^{\infty }\gamma _{n}z^{n}$. The second Hankel determinant for logarithmic coefficients is defined by

$$ \begin{align*} H_{2,2}(F_f/2) = \begin{vmatrix} \gamma_2 & \gamma_3 \\ \gamma_3 & \gamma_4 \end{vmatrix} =\gamma_2\gamma_4 -\gamma_3^2. \end{align*} $$

We obtain sharp upper bounds of the second Hankel determinant of logarithmic coefficients for starlike and convex functions.

Given a Gromov hyperbolic domain $G\subsetneq \mathbb{R}^n$ with uniformly perfect Gromov boundary, Zhou and Rasila recently proved that for all quasiconformal homeomorphisms $\psi\colon G\to G$ with identity value on the Gromov boundary, the quasihyperbolic displacement $k_G(x,\psi(x))$ for all $x\in G$ is bounded above. In this paper, we generalize this result and establish Teichmüller displacement theorem for quasi-isometries of Gromov hyperbolic spaces in a quantitative way. As applications, we obtain its connections to bilipschitz extensions of certain Gromov hyperbolic spaces.

We prove an effective estimate with a power saving error term for the number of square-tiled surfaces in a connected component of a stratum of quadratic differentials whose vertical and horizontal foliations belong to prescribed mapping class group orbits and which have at most L squares. This result strengthens asymptotic counting formulas in the work of Delecroix, Goujard, Zograf, Zorich, and the author.

The possibilities for limit functions on a Fatou component for the iteration of a single polynomial or rational function are well understood and quite restricted. In non-autonomous iteration, where one considers compositions of arbitrary polynomials with suitably bounded degrees and coefficients, one should observe a far greater range of behavior. We show this is indeed the case and we exhibit a bounded sequence of quadratic polynomials which has a bounded Fatou component on which one obtains as limit functions every member of the classical Schlicht family of normalized univalent functions on the unit disc. The proof is based on quasiconformal surgery and the use of high iterates of a quadratic polynomial with a Siegel disc which closely approximate the identity on compact subsets. Careful bookkeeping using the hyperbolic metric is required to control the errors in approximating the desired limit functions and ensure that these errors ultimately tend to zero.

We define balanced self-similar quasi-round carpets and compare the carpet moduli of some path families relating to such a carpet. Then, using some known results on quasiconformal geometry of carpets, we prove that the group of quasisymmetric self-homeomorphisms of every balanced self-similar quasi-round carpet is finite. Furthermore, we prove that some balanced self-similar carpets in the unit square with strong geometric symmetry are quasisymmetrically rigid by using the quasisymmetry of weak tangents of carpets.

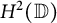
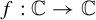
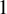
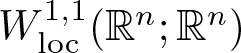
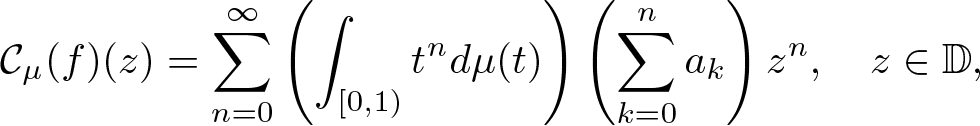
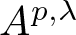
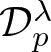
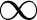
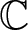
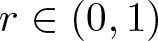
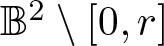
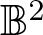
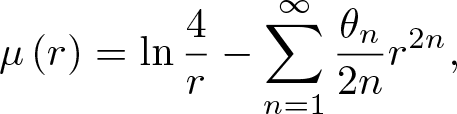
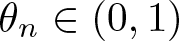
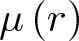
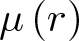
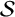
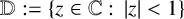
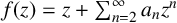
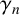
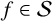
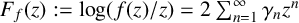
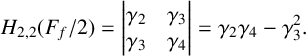
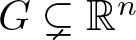
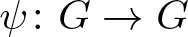
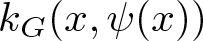
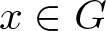
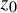
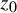
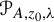Let A be a rational function of one complex variable of degree at least two, and $z_0$ its repelling fixed point with the multiplier $\unicode{x3bb} .$ A Poincaré function associated with $z_0$ is a function meromorphic on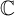 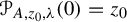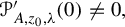${\mathbb C}$ such that , and 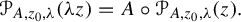In this paper, we study the following problem: given Poincaré functions 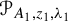and 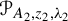, find out if there is an algebraic relation 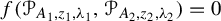between them and, if such a relation exists, describe the corresponding algebraic curve $f(x,y)=0.$ We provide a solution, which can be viewed as a refinement of the classical theorem of Ritt about commuting rational functions. We also reprove and extend previous results concerning algebraic dependencies between Böttcher functions.

We give a new proof of a theorem of Bell and Coons [‘Transcendence tests for Mahler functions’, Proc. Amer. Math. Soc. 145(3) (2017), 1061–1070] on the leading order radial asymptotics of Mahler functions that are the generating functions of regular sequences. Our method allows us to provide a description of the oscillations whose existence was shown by Bell and Coons. This extends very recent results of Poulet and Rivoal [‘Radial behavior of Mahler functions’, Int. J. Number Theory, to appear].