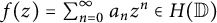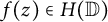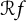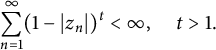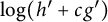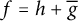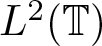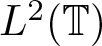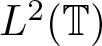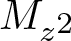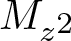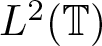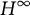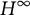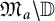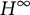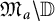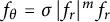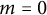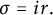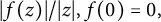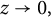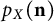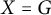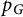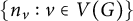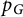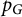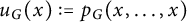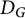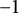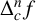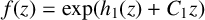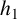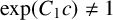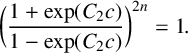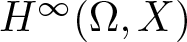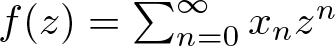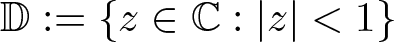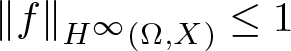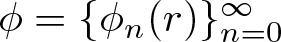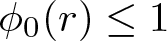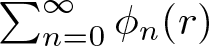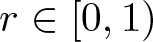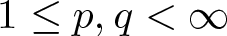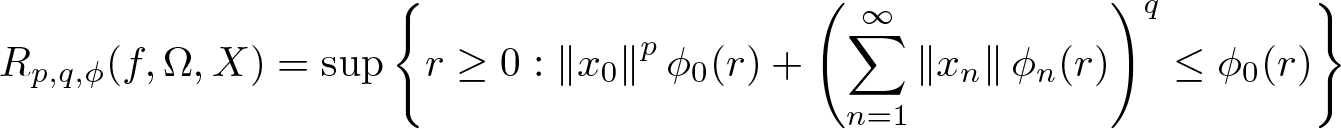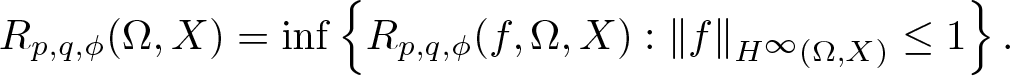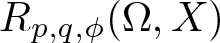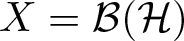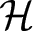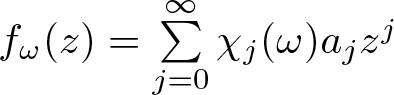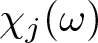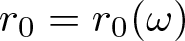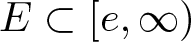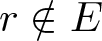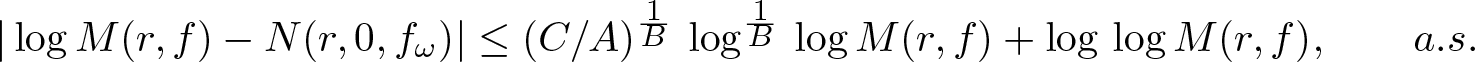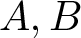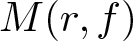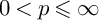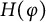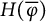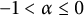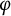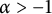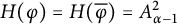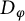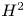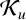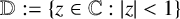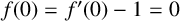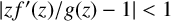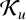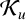Refine listing
Actions for selected content:
543 results in 30xxx
Karamata’s theorem for regularized Cauchy transforms
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 26 January 2024, pp. 1431-1491
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A characterization of random analytic functions satisfying Blaschke-type conditions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 17 January 2024, pp. 670-679
- Print publication:
- September 2024
-
- Article
- Export citation
Integral mean estimates for univalent and locally univalent harmonic mappings
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 15 January 2024, pp. 655-669
- Print publication:
- September 2024
-
- Article
- Export citation
Commutants and complex symmetry of finite Blaschke product multiplication operator in
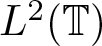 $L^2(\mathbb{T})$
$L^2(\mathbb{T})$
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 11 January 2024, pp. 261-286
-
- Article
- Export citation
On the Extension of Bounded Holomorphic Maps from Gleason Parts of the Maximal Ideal Space of
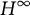 $H^\infty $
$H^\infty $
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 08 January 2024, pp. 624-632
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Symmetric and antisymmetric tensor products for the function-theoretic operator theorist
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 22 December 2023, pp. 324-346
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nonlinear Beltrami equation: lower estimates of Schwarz lemma’s type
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 29 November 2023, pp. 533-543
- Print publication:
- September 2024
-
- Article
- Export citation
Symmetrized and non-symmetrized asymptotic mean value Laplacian in metric measure spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 28 November 2023, pp. 916-953
- Print publication:
- June 2025
-
- Article
- Export citation
The blowup-polynomial of a metric space: connections to stable polynomials, graphs and their distance spectra
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 09 November 2023, pp. 2073-2114
- Print publication:
- December 2024
-
- Article
- Export citation
LINEAR GROWTH OF TRANSLATION LENGTHS OF RANDOM ISOMETRIES ON GROMOV HYPERBOLIC SPACES AND TEICHMÜLLER SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 1751-1795
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE DIFFERENCE ANALOGUE OF THE TUMURA–HAYMAN–CLUNIE THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 145-154
- Print publication:
- August 2024
-
- Article
- Export citation
Bohr radius for Banach spaces on simply connected domains
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 03 November 2023, pp. 113-141
-
- Article
- Export citation
Normal families and quasiregular mappings
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 23 October 2023, pp. 79-112
-
- Article
- Export citation
Inequalities concerning maximum modulus and zeros of random entire functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 19 October 2023, pp. 57-78
-
- Article
- Export citation
HARMONIC-MEASURE DISTRIBUTION FUNCTIONS AND RELATED FUNCTIONS FOR SIMPLY CONNECTED AND MULTIPLY CONNECTED TWO-DIMENSIONAL REGIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 06 October 2023, pp. 163-164
- Print publication:
- February 2024
-
- Article
-
- You have access
- HTML
- Export citation
MULTIPLIERS AND CHARACTERIZATION OF THE DUAL OF NEVANLINNA-TYPE SPACES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 253 / March 2024
- Published online by Cambridge University Press:
- 07 September 2023, pp. 216-240
- Print publication:
- March 2024
-
- Article
- Export citation
Sub-Bergman Hilbert spaces on the unit disk III
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 22 August 2023, pp. 1520-1537
- Print publication:
- October 2024
-
- Article
- Export citation
Uniform spectral gap and orthogeodesic counting for strong convergence of Kleinian groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 04 August 2023, e68
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Schatten class composition operators on the Hardy space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 24 July 2023, pp. 1364-1377
- Print publication:
- October 2024
-
- Article
- Export citation
ON CERTAIN CLOSE-TO-CONVEX FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 17 July 2023, pp. 365-375
- Print publication:
- April 2024
-
- Article
- Export citation