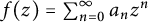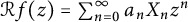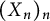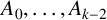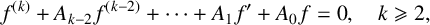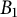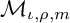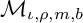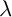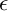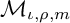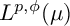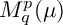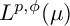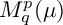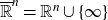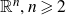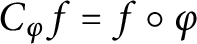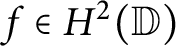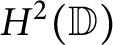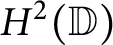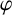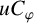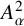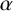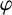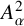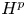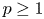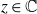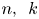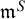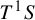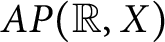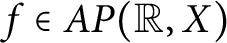Refine listing
Actions for selected content:
543 results in 30xxx
Two problems on random analytic functions in Fock spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 08 July 2022, pp. 1176-1198
- Print publication:
- August 2023
-
- Article
- Export citation
DESCRIPTION OF GROWTH AND OSCILLATION OF SOLUTIONS OF COMPLEX LDE’S
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 16 June 2022, pp. 145-171
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Volterra-type operators on the minimal Möbius-invariant space
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 13 June 2022, pp. 509-524
- Print publication:
- June 2023
-
- Article
- Export citation
FRACTIONAL TYPE MARCINKIEWICZ INTEGRAL AND ITS COMMUTATOR ON NONHOMOGENEOUS SPACES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 248 / December 2022
- Published online by Cambridge University Press:
- 03 June 2022, pp. 801-822
- Print publication:
- December 2022
-
- Article
- Export citation
Conformally invariant complete metrics
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 30 May 2022, pp. 273-300
- Print publication:
- March 2023
-
- Article
- Export citation
On the derivative of a polynomial
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 24 May 2022, pp. 303-310
-
- Article
- Export citation
Analytic Besov spaces, approximation, and closed ideals
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 13 May 2022, pp. 259-268
- Print publication:
- March 2023
-
- Article
- Export citation
Dynamics of generalised exponential maps
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 21 April 2022, pp. 123-136
- Print publication:
- January 2023
-
- Article
- Export citation
Model spaces invariant under composition operators
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 25 March 2022, pp. 204-217
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COMPACT AND HILBERT–SCHMIDT WEIGHTED COMPOSITION OPERATORS ON WEIGHTED BERGMAN SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 22 March 2022, pp. 208-225
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generalized Bloch type periodicity and applications to semi-linear differential equations in banach spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 08 March 2022, pp. 326-355
-
- Article
- Export citation
Approximation numbers of composition operators on weighted besov spaces of analytic functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 28 February 2022, pp. 311-325
-
- Article
- Export citation
On the roots of polynomials with log-convex coefficients
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 15 February 2022, pp. 470-493
- Print publication:
- April 2023
-
- Article
- Export citation
Distinguishing endpoint sets from Erdős space
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 3 / November 2022
- Published online by Cambridge University Press:
- 15 February 2022, pp. 635-646
- Print publication:
- November 2022
-
- Article
- Export citation
CARLSON–GRIFFITHS THEORY FOR COMPLETE KÄHLER MANIFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 14 February 2022, pp. 2337-2365
- Print publication:
- September 2023
-
- Article
- Export citation
On meromorphic solutions of functional-differential equations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 10 February 2022, pp. 263-278
-
- Article
- Export citation
Oscillating simply connected wandering domains
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 4 / April 2023
- Published online by Cambridge University Press:
- 09 February 2022, pp. 1239-1268
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hausdorff dimension of escaping sets of meromorphic functions II
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 03 February 2022, pp. 1471-1491
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Distribution in the unit tangent bundle of the geodesics of given type
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 3 / March 2023
- Published online by Cambridge University Press:
- 24 January 2022, pp. 887-903
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on spaces of almost periodic functions with values in Banach spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 18 January 2022, pp. 953-962
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation