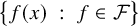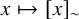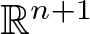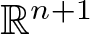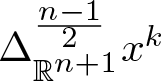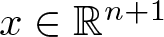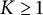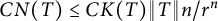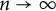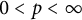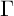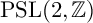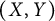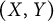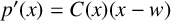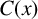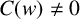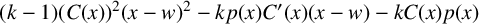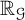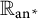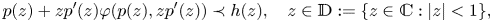Refine listing
Actions for selected content:
543 results in 30xxx
Uncertainty principles in holomorphic function spaces on the unit ball
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 10 July 2023, pp. 122-136
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Landau-type theorems for certain bounded bi-analytic functions and biharmonic mappings
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 05 July 2023, pp. 152-165
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sparse analytic systems
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 04 July 2023, e58
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Fueter-Sce mapping and the Clifford–Appell polynomials
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 28 June 2023, pp. 642-688
-
- Article
- Export citation
Bohr operator on operator-valued polyanalytic functions on simply connected domains
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 26 June 2023, pp. 1411-1422
- Print publication:
- December 2023
-
- Article
- Export citation
Schwarz lemma for real harmonic functions onto surfaces with non-negative Gaussian curvature
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 15 June 2023, pp. 516-531
-
- Article
- Export citation
Refined Bohr inequalities for certain classes of functions: analytic, univalent, and convex
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 09 June 2023, pp. 9-25
- Print publication:
- March 2024
-
- Article
- Export citation
On the condition number of a Kreiss matrix
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 29 May 2023, pp. 1376-1390
- Print publication:
- December 2023
-
- Article
- Export citation
THE THIRD HANKEL DETERMINANT FOR INVERSE COEFFICIENTS OF CONVEX FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 02 May 2023, pp. 94-100
- Print publication:
- February 2024
-
- Article
- Export citation
Improved Bloch and Landau constants for meromorphic functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 28 April 2023, pp. 1269-1273
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Composition operators on weighted analytic spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 17 April 2023, pp. 1213-1230
- Print publication:
- December 2023
-
- Article
- Export citation
Multiply connected wandering domains of meromorphic functions: the pursuit of uniform internal dynamics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 3 / March 2024
- Published online by Cambridge University Press:
- 11 April 2023, pp. 727-748
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
KRONECKER LIMIT FUNCTIONS AND AN EXTENSION OF THE ROHRLICH–JENSEN FORMULA
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 252 / December 2023
- Published online by Cambridge University Press:
- 11 April 2023, pp. 810-841
- Print publication:
- December 2023
-
- Article
- Export citation
General Toeplitz kernels and
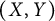 $(X,Y)$-invariance
$(X,Y)$-invariance
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 27 March 2023, pp. 680-706
- Print publication:
- April 2024
-
- Article
- Export citation
BOUNDS FOR FUNCTIONALS DEFINED ON A CERTAIN CLASS OF MEROMORPHIC FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 03 March 2023, pp. 101-109
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE NUMBER OF REAL ZEROS OF POLYNOMIALS OF EVEN DEGREE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 27 February 2023, pp. 89-93
- Print publication:
- February 2024
-
- Article
- Export citation
Multisummability for generalized power series
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 27 February 2023, pp. 458-494
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On a class of difference operator and its applications to a family of analytic functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 27 February 2023, pp. 248-258
- Print publication:
- February 2024
-
- Article
- Export citation
A new inner approach for differential subordinations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 10 February 2023, pp. 259-272
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Liouville property and quasi-isometries on negatively curved Riemannian surfaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 10 February 2023, pp. 131-153
- Print publication:
- February 2024
-
- Article
- Export citation