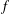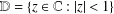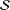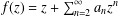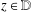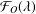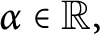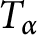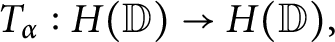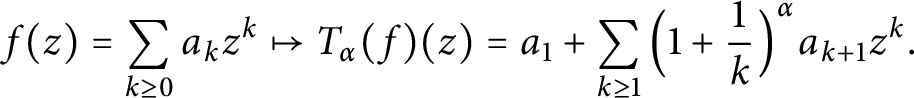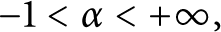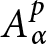Refine listing
Actions for selected content:
543 results in 30xxx
ON THE DIFFERENCE OF COEFFICIENTS OF OZAKI CLOSE-TO-CONVEX FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 18 June 2020, pp. 124-131
- Print publication:
- February 2021
-
- Article
- Export citation
Growth of frequently hypercyclic functions for some weighted Taylor shifts on the unit disc
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 11 June 2020, pp. 264-281
- Print publication:
- June 2021
-
- Article
- Export citation
COARSE AND FINE GEOMETRY OF THE THURSTON METRIC
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 26 May 2020, e28
-
- Article
-
- You have access
- Open access
- Export citation
Restrictions on meromorphic solutions of Fermat type equations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 3 / August 2020
- Published online by Cambridge University Press:
- 08 May 2020, pp. 654-665
-
- Article
- Export citation
Entire solutions of a variation of the eikonal equation and related PDEs
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 3 / August 2020
- Published online by Cambridge University Press:
- 07 May 2020, pp. 697-708
-
- Article
- Export citation
Hyperbolic metric and membership of conformal maps in the Bergman space
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 06 May 2020, pp. 174-181
- Print publication:
- March 2021
-
- Article
- Export citation
The Dual of the Compressed Shift
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 17 April 2020, pp. 98-111
- Print publication:
- March 2021
-
- Article
- Export citation
VANISHING COEFFICIENTS IN QUOTIENTS OF THETA FUNCTIONS OF MODULUS FIVE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 27 March 2020, pp. 387-398
- Print publication:
- December 2020
-
- Article
- Export citation
ENUMERATION OF MEANDERS AND MASUR–VEECH VOLUMES
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 23 March 2020, e4
-
- Article
-
- You have access
- Open access
- Export citation
ON THE HARMONIC ZYGMUND SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 11 March 2020, pp. 466-476
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
SPHERICALIZATION AND FLATTENING PRESERVE UNIFORM DOMAINS IN NONLOCALLY COMPACT METRIC SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 27 February 2020, pp. 68-89
- Print publication:
- February 2022
-
- Article
- Export citation
Radial symmetry of minimizers to the weighted Dirichlet energy
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 20 February 2020, pp. 169-186
- Print publication:
- February 2021
-
- Article
- Export citation
ON THE PERIODICITY OF TRANSCENDENTAL ENTIRE FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 13 February 2020, pp. 453-465
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
DEGREE-ONE MAHLER FUNCTIONS: ASYMPTOTICS, APPLICATIONS AND SPECULATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 05 February 2020, pp. 399-409
- Print publication:
- December 2020
-
- Article
- Export citation
SQUARE-INTEGRABILITY OF THE MIRZAKHANI FUNCTION AND STATISTICS OF SIMPLE CLOSED GEODESICS ON HYPERBOLIC SURFACES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 04 February 2020, e9
-
- Article
-
- You have access
- Open access
- Export citation
Short closed geodesics with self-intersections
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 3 / November 2020
- Published online by Cambridge University Press:
- 24 January 2020, pp. 623-638
- Print publication:
- November 2020
-
- Article
- Export citation
On slow escaping and non-escaping points of quasimeromorphic mappings
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 22 January 2020, pp. 1190-1216
- Print publication:
- April 2021
-
- Article
- Export citation
ON A CLOSE-TO-CONVEX ANALOGUE OF CERTAIN STARLIKE FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 22 January 2020, pp. 268-281
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
A note on the topology of escaping endpoints
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 13 January 2020, pp. 1156-1159
- Print publication:
- April 2021
-
- Article
- Export citation
QUASICONFORMAL HARMONIC MAPPINGS BETWEEN DOMAINS CONTAINING INFINITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 109-117
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation