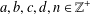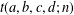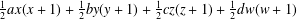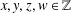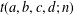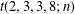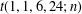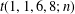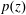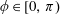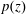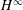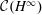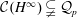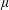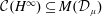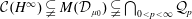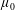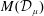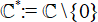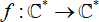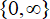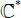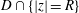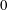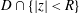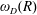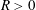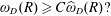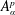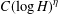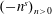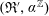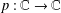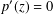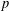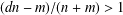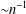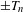Refine listing
Actions for selected content:
543 results in 30xxx
TRANSFORMATION FORMULAS FOR THE NUMBER OF REPRESENTATIONS OF
 $n$ BY LINEAR COMBINATIONS OF FOUR TRIANGULAR NUMBERS
$n$ BY LINEAR COMBINATIONS OF FOUR TRIANGULAR NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 39-49
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Sector Analogue of the Gauss–Lucas Theorem
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 12 December 2019, pp. 318-338
- Print publication:
- April 2021
-
- Article
- Export citation
ASYMPTOTICS OF A GAUSS HYPERGEOMETRIC FUNCTION WITH TWO LARGE PARAMETERS: A NEW CASE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 62 / Issue 4 / October 2020
- Published online by Cambridge University Press:
- 10 December 2019, pp. 446-452
-
- Article
-
- You have access
- Export citation
The Range of the Cesàro Operator Acting on
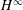 $H^{\infty }$
$H^{\infty }$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 December 2019, pp. 633-642
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
Escaping Fatou components of transcendental self-maps of the punctured plane
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 28 November 2019, pp. 265-289
- Print publication:
- March 2021
-
- Article
- Export citation
POWERS OF COMPOSITION OPERATORS: ASYMPTOTIC BEHAVIOUR ON BERGMAN, DIRICHLET AND BLOCH SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 27 November 2019, pp. 289-320
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
On a Property of Harmonic Measure on Simply Connected Domains
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 22 November 2019, pp. 297-317
- Print publication:
- April 2021
-
- Article
- Export citation
Derivatives of Blaschke Products and Model Space Functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 12 November 2019, pp. 716-725
- Print publication:
- December 2020
-
- Article
- Export citation
On Selberg’s eigenvalue conjecture for moduli spaces of abelian differentials
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 12 / December 2019
- Published online by Cambridge University Press:
- 30 October 2019, pp. 2354-2398
- Print publication:
- December 2019
-
- Article
- Export citation
ALGEBRAIC VALUES OF CERTAIN ANALYTIC FUNCTIONS DEFINED BY A CANONICAL PRODUCT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 08 October 2019, pp. 415-425
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
Entropy of transcendental entire functions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 07 October 2019, pp. 338-348
- Print publication:
- February 2021
-
- Article
- Export citation
Expansions of the Real Field by Canonical Products
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 October 2019, pp. 506-521
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
BOUNDARY SCHWARZ LEMMA FOR SOLUTIONS TO NONHOMOGENEOUS BIHARMONIC EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 09 September 2019, pp. 470-478
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
A STABILITY VERSION OF THE GAUSS–LUCAS THEOREM AND APPLICATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 05 September 2019, pp. 262-269
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
Potential flow over a submerged rectangular obstacle: Consequences for initiation of boulder motion
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 05 September 2019, pp. 646-681
-
- Article
- Export citation
Persistence probability of a random polynomial arising from evolutionary game theory
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 01 October 2019, pp. 870-890
- Print publication:
- September 2019
-
- Article
- Export citation
Equality case for an elliptic area condenser inequality and a related Schwarz type lemma
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 19 August 2019, pp. 91-104
-
- Article
- Export citation
Commuting rational functions revisited
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 15 August 2019, pp. 295-320
- Print publication:
- January 2021
-
- Article
- Export citation
Embedding Theorems for Dirichlet Type Spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 22 July 2019, pp. 106-117
- Print publication:
- March 2020
-
- Article
-
- You have access
- Export citation
ON SOME SUBCLASSES OF HARMONIC MAPPINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 10 July 2019, pp. 130-140
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation