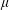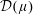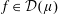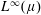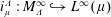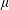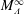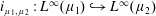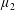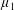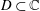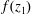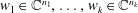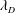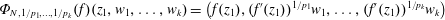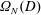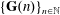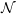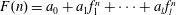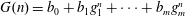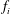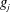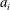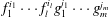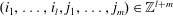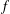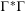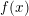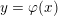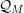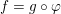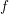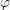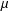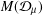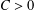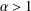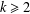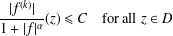Refine listing
Actions for selected content:
543 results in 30xxx
Explicit asymptotics for certain single and double exponential sums
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 22 January 2019, pp. 607-632
- Print publication:
- April 2020
-
- Article
- Export citation
Cyclicity in Dirichlet Spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 11 January 2019, pp. 247-257
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Embeddings of Müntz Spaces in
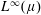 $L^{\infty }(\unicode[STIX]{x1D707})$
$L^{\infty }(\unicode[STIX]{x1D707})$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 1-9
- Print publication:
- March 2019
-
- Article
-
- You have access
- Export citation
Extension Operators for Biholomorphic Mappings
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 671-679
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
Determinant of the Laplacian on Tori of Constant Positive Curvature with one Conical Point
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 04 January 2019, pp. 341-347
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
QUANTITATIVE PROPERTIES OF MEROMORPHIC SOLUTIONS TO SOME DIFFERENTIAL-DIFFERENCE EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 26 December 2018, pp. 250-261
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
LARGE-SCALE SUBLINEARLY LIPSCHITZ GEOMETRY OF HYPERBOLIC SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 19 December 2018, pp. 1831-1876
- Print publication:
- November 2020
-
- Article
- Export citation
Approximating the Riemann Zeta-function by Polynomials with Restricted Zeros
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 17 December 2018, pp. 475-478
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
Manhattan curves for hyperbolic surfaces with cusps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 7 / July 2020
- Published online by Cambridge University Press:
- 04 December 2018, pp. 1843-1874
- Print publication:
- July 2020
-
- Article
- Export citation
Range Spaces of Co-Analytic Toeplitz Operators
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 70 / Issue 6 / 01 December 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1261-1283
- Print publication:
- 01 December 2018
-
- Article
-
- You have access
- Export citation
The Quotient Problem for Entire Functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 26 October 2018, pp. 479-489
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
ON OZAKI CLOSE-TO-CONVEX FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 20 September 2018, pp. 89-100
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
DOUBLING TROPICAL
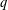 $q$ -DIFFERENCE ANALOGUE OF THE LEMMA ON THE LOGARITHMICDERIVATIVE
$q$ -DIFFERENCE ANALOGUE OF THE LEMMA ON THE LOGARITHMICDERIVATIVE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 12 September 2018, pp. 474-480
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
INVERSE SPECTRAL THEORY FOR A CLASS OF NON-COMPACT HANKEL OPERATORS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 1 / 2019
- Published online by Cambridge University Press:
- 06 September 2018, pp. 132-156
- Print publication:
- 2019
-
- Article
- Export citation
On a Criterion of Local Invertibility and Conformality for Slice Regular Quaternionic Functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 28 August 2018, pp. 97-105
-
- Article
- Export citation
Composite quasianalytic functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 9 / September 2018
- Published online by Cambridge University Press:
- 17 August 2018, pp. 1960-1973
- Print publication:
- September 2018
-
- Article
- Export citation
CONTINUITY OF ROOTS, REVISITED
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 15 August 2018, pp. 448-455
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
MÖBIUS INVARIANT FUNCTION SPACES AND DIRICHLET SPACES WITH SUPERHARMONIC WEIGHTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 106 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 12 July 2018, pp. 1-18
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
A STRUCTURED DESCRIPTION OF THE GENUS SPECTRUM OF ABELIAN p-GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 10 July 2018, pp. 381-423
- Print publication:
- May 2019
-
- Article
-
- You have access
- Export citation
DIFFERENTIAL INEQUALITIES AND A MARTY-TYPE CRITERION FOR QUASI-NORMALITY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 105 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 18 June 2018, pp. 34-45
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation