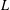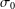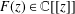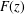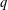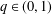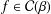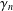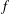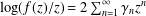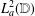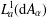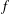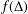Refine listing
Actions for selected content:
543 results in 30xxx
ON ALGEBRAIC DIFFERENTIAL EQUATIONS FOR THE GAMMA FUNCTION AND
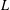 $L$ -FUNCTIONS IN THE EXTENDED SELBERG CLASS
$L$ -FUNCTIONS IN THE EXTENDED SELBERG CLASS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 36-43
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
TRANSCENDENCE OVER MEROMORPHIC FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 393-399
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
COEFFICIENT ESTIMATES FOR SOME CLASSES OF FUNCTIONS ASSOCIATED WITH
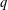 $q$ -FUNCTION THEORY
$q$ -FUNCTION THEORY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 06 March 2017, pp. 446-456
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
A GENERALISATION OF THE CLUNIE–SHEIL-SMALL THEOREM II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 02 March 2017, pp. 457-466
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
Hyperbolic Metric and Multiply Connected Wandering Domains of Meromorphic Functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 30 January 2017, pp. 787-810
-
- Article
- Export citation
SYMMETRIC CROSSCAP NUMBER OF GROUPS OF ORDER LESS THAN OR EQUAL TO 63
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 23 December 2016, pp. 145-156
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
SOME NORMALITY CRITERIA AND A COUNTEREXAMPLE TO THE CONVERSE OF BLOCH’S PRINCIPLE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 23 November 2016, pp. 238-249
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
INVARIANCE OF THE COEFFICIENTS OF STRONGLY CONVEX FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 23 November 2016, pp. 436-445
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
LOGARITHMIC COEFFICIENTS OF SOME CLOSE-TO-CONVEX FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 02 November 2016, pp. 228-237
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
POLYGONAL QUASICONFORMAL MAPPINGS AND CHORD-ARC CURVES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 02 November 2016, pp. 66-72
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
THE HILBERT–SCHMIDT NORM OF A COMPOSITION OPERATOR ON THE BERGMAN SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 02 November 2016, pp. 250-259
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
GENERALIZED MORREY SPACES OVER NONHOMOGENEOUS METRIC MEASURE SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 27 October 2016, pp. 268-278
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
Extremal Beltrami Differentials of Non-Landslide Type
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 25 October 2016, pp. 519-526
-
- Article
- Export citation
LIMITS OF FRACTIONAL DERIVATIVES AND COMPOSITIONS OF ANALYTIC FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 28 September 2016, pp. 104-115
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
QUASICONFORMAL EXTENSIONS OF HARMONIC MAPPINGS WITH A COMPLEX PARAMETER
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 19 September 2016, pp. 307-315
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
NONDECREASABLE AND WEAKLY NONDECREASABLE DILATATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 19 September 2016, pp. 420-434
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
RADII OF HARMONIC MAPPINGS IN THE PLANE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 08 July 2016, pp. 331-347
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
Fischer Decomposition and Cauchy–Kovalevskaya Extension in Fractional Clifford Analysis: The Riemann–Liouville Case
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 13 June 2016, pp. 251-272
-
- Article
- Export citation
ON THE FREQUENT UNIVERSALITY OF UNIVERSAL TAYLOR SERIES IN THE COMPLEX PLANE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 109-117
- Print publication:
- January 2017
-
- Article
-
- You have access
- Export citation
A TOWER OF RIEMANN SURFACES WHICH CANNOT BE DEFINED OVER THEIR FIELD OF MODULI
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 379-393
- Print publication:
- May 2017
-
- Article
-
- You have access
- Export citation