Refine listing
Actions for selected content:
543 results in 30xxx
About the zeros of some entire functions and their derivatives
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 68 / Issue 2 / April 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 165-169
- Print publication:
- April 2000
-
- Article
-
- You have access
- Export citation
On Symmetric Quasicircles
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 68 / Issue 1 / February 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 131-144
- Print publication:
- February 2000
-
- Article
-
- You have access
- Export citation
Functions of bounded expansion: normal and Bloch functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 2 / April 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 168-188
- Print publication:
- April 1999
-
- Article
-
- You have access
- Export citation
On the value distribution of iterated entire functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 1 / February 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 18-31
- Print publication:
- February 1999
-
- Article
-
- You have access
- Export citation
Integral means on radially weighted spaces of analytic functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 1 / August 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 68-83
- Print publication:
- August 1998
-
- Article
-
- You have access
- Export citation
On singular boundary points of complex functions
- Part of
-
- Journal:
- Mathematika / Volume 45 / Issue 1 / June 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 119-133
- Print publication:
- June 1998
-
- Article
- Export citation
Representation formulas for entire functions of exponential type and generalized bernoulli polynomials
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 3 / June 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 307-316
- Print publication:
- June 1998
-
- Article
-
- You have access
- Export citation
Products of spherical derivatives and normal functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 2 / April 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 231-246
- Print publication:
- April 1998
-
- Article
-
- You have access
- Export citation
Continued Fraction Analysis of the Duration of an Excursion in an M/M/∞ System
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 1 / March 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 165-183
- Print publication:
- March 1998
-
- Article
- Export citation
Truncated tetrahedra and their reflection groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 1 / February 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 54-72
- Print publication:
- February 1998
-
- Article
-
- You have access
- Export citation
Radial variation of functions in Dirichlet-type spaces
- Part of
-
- Journal:
- Mathematika / Volume 44 / Issue 2 / December 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 267-277
- Print publication:
- December 1997
-
- Article
- Export citation
Even compositions of entire functions and related matters
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 63 / Issue 2 / October 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 225-237
- Print publication:
- October 1997
-
- Article
-
- You have access
- Export citation
Functions with unbounded ∂-derivative and their boundary functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 63 / Issue 1 / August 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 100-109
- Print publication:
- August 1997
-
- Article
-
- You have access
- Export citation
Value distribution of certain monomials of algebroid functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 62 / Issue 3 / June 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 398-404
- Print publication:
- June 1997
-
- Article
-
- You have access
- Export citation
Analysis of a two-queue model with Bernoulli schedules
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 1 / March 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 176-191
- Print publication:
- March 1997
-
- Article
- Export citation
Sharp extensions of Bernstein's inequality to rational spaces
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 2 / December 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 413-423
- Print publication:
- December 1996
-
- Article
- Export citation
On convex and starlike functions in a sector
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 3 / June 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 363-368
- Print publication:
- June 1996
-
- Article
-
- You have access
- Export citation
Coefficients of an analytic function subordination class determined by rotations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 2 / April 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 245-254
- Print publication:
- April 1996
-
- Article
-
- You have access
- Export citation
On the logarithmic coefficients of close-to-convex functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 1 / February 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-6
- Print publication:
- February 1996
-
- Article
-
- You have access
- Export citation
Matrix transformations of series of orthogonal polynomials
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 2 / December 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 427-443
- Print publication:
- December 1995
-
- Article
- Export citation
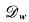 to denote the Dirichlettype space of functions
to denote the Dirichlettype space of functions 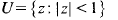 and for which
and for which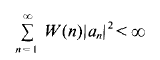
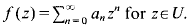 If
If 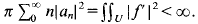 Note also that
Note also that 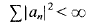 for every
for every 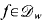 so, by Fatu's theoreum, every function in
so, by Fatu's theoreum, every function in 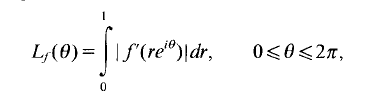
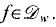
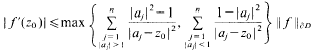
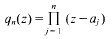

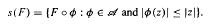
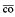
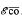
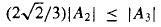 for
for 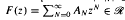 . We also prove that if
. We also prove that if 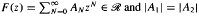 , then
, then 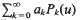 given by
given by 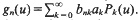 . We establish necessary and sufficient conditions on the matrix (
. We establish necessary and sufficient conditions on the matrix (