Refine listing
Actions for selected content:
41 results in 51Exx
Buildings, spiders, and geometric Satake
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 11 / November 2013
- Published online by Cambridge University Press:
- 10 July 2013, pp. 1871-1912
- Print publication:
- November 2013
-
- Article
- Export citation
KAKEYA SETS OVER NON-ARCHIMEDEAN LOCAL RINGS
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 2 / July 2013
- Published online by Cambridge University Press:
- 28 March 2013, pp. 257-266
- Print publication:
- July 2013
-
- Article
- Export citation
AUTOMORPHISMS AND OPPOSITION IN TWIN BUILDINGS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 08 March 2013, pp. 189-201
- Print publication:
- April 2013
-
- Article
-
- You have access
- Export citation
AN EIGENSPACE OF LARGE DIMENSION FOR A HECKE ALGEBRA ON AN
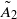 BUILDING
BUILDING
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 91 / Issue 1 / August 2011
- Published online by Cambridge University Press:
- 28 September 2011, pp. 29-54
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
THE KAKEYA SET AND MAXIMAL CONJECTURES FOR ALGEBRAIC VARIETIES OVER FINITE FIELDS
- Part of
-
- Journal:
- Mathematika / Volume 56 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 10 December 2009, pp. 1-25
- Print publication:
- January 2010
-
- Article
- Export citation
SEMIFIELDS ARISING FROM IRREDUCIBLE SEMILINEAR TRANSFORMATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 85 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 333-339
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
ELATION GENERALIZED QUADRANGLES FOR WHICH THE NUMBER OF LINES ON A POINT IS THE SUCCESSOR OF A PRIME
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 85 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 289-303
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
Laguerre geometries and some connections to generalized quadrangles
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 3 / December 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 335-356
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
Large doubly transitive orbits on a line
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 2 / October 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 227-270
- Print publication:
- October 2007
-
- Article
-
- You have access
- Export citation
Finite Fourier series and ovals in PG(2, 2h)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 1 / August 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 21-34
- Print publication:
- August 2006
-
- Article
-
- You have access
- Export citation
Some remarks on flocks
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 3 / June 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 329-344
- Print publication:
- June 2004
-
- Article
-
- You have access
- Export citation
Daisy structure in Desarguesian projective planes
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 2 / April 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 145-154
- Print publication:
- April 2003
-
- Article
-
- You have access
- Export citation
Radon transform on affine buildings of rank three
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 1 / February 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 66-89
- Print publication:
- February 1999
-
- Article
-
- You have access
- Export citation
Application of the Bruhat-Tits tree of SU3(h) to some Ã2 groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 3 / June 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 329-344
- Print publication:
- June 1998
-
- Article
-
- You have access
- Export citation
Sporadic group geometries and the action of involutions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 1 / August 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 35-48
- Print publication:
- August 1994
-
- Article
-
- You have access
- Export citation
Extensions of G-posets and Quillen's complex
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 1 / August 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 60-75
- Print publication:
- August 1994
-
- Article
-
- You have access
- Export citation
Harmonic analysis for groups acting on triangle buildings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 3 / June 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 345-383
- Print publication:
- June 1994
-
- Article
-
- You have access
- Export citation
On Pascal ovals
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 54 / Issue 1 / February 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 61-69
- Print publication:
- February 1993
-
- Article
-
- You have access
- Export citation
A dual approach to embedding the complement of two lines in a finite projective plane
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 51 / Issue 3 / December 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 426-435
- Print publication:
- December 1991
-
- Article
-
- You have access
- Export citation
Collineation groups preserving an oval in a projective place of odd order
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 48 / Issue 1 / February 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 156-170
- Print publication:
- February 1990
-
- Article
-
- You have access
- Export citation
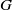
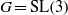
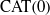
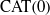
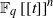
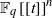
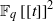
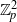
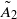 BUILDING
BUILDING
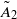 and let 𝔸 be its fundamental apartment. We consider the set 𝕌
and let 𝔸 be its fundamental apartment. We consider the set 𝕌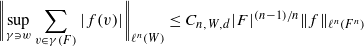
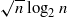 different nondesarguesian planes.
different nondesarguesian planes.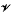 be its set of vertices. We study a commutative algebra
be its set of vertices. We study a commutative algebra 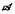 of ‘averaging’ operators acting on the space of complex valued functions on
of ‘averaging’ operators acting on the space of complex valued functions on 