Refine listing
Actions for selected content:
346 results in 20Exx
Nilpotent and semi-n-abelian groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 3 / October 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 262-268
- Print publication:
- October 1981
-
- Article
-
- You have access
- Export citation
The laws of some metabelian varieties
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 4 / April 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 469-472
- Print publication:
- April 1981
-
- Article
-
- You have access
- Export citation
Separating conjugates in amalgamated free products and HNN extensions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 29 / Issue 1 / February 1980
- Published online by Cambridge University Press:
- 09 April 2009, pp. 35-51
- Print publication:
- February 1980
-
- Article
-
- You have access
- Export citation
Completions of certain nilpotent groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 28 / Issue 4 / December 1979
- Published online by Cambridge University Press:
- 09 April 2009, pp. 461-470
- Print publication:
- December 1979
-
- Article
-
- You have access
- Export citation
Direct decompositions of groups with finitely generated commutator quotient group
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 28 / Issue 3 / November 1979
- Published online by Cambridge University Press:
- 09 April 2009, pp. 315-320
- Print publication:
- November 1979
-
- Article
-
- You have access
- Export citation
Splitting theorems in abelian-by-hypercyclic groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 25 / Issue 1 / February 1978
- Published online by Cambridge University Press:
- 09 April 2009, pp. 71-91
- Print publication:
- February 1978
-
- Article
-
- You have access
- Export citation
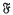 is a saturated formation of finite soluble groups and
is a saturated formation of finite soluble groups and 