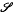If ω ≡ 1 is a group law implying virtual nilpotence in every finitely generated metabelian group satisfying it, then it implies virtual nilpotence for the finitely generated groups of a large class of groups including all residually or locally soluble-or-finite groups. In fact the groups of satisfying such a law are all nilpotent-by-finite exponent where the nilpotency class and exponent in question are both bounded above in terms of the length of ω alone. This yields a dichotomy for words. Finally, if the law ω ≡ 1 satisfies a certain additional condition—obtaining in particular for any monoidal or Engel law—then the conclusion extends to the much larger class consisting of all ‘locally graded’ groups.

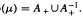Let Γ be a free noncommutative group with free generating set A+. Let μ ∈ ℓ1(Γ) be real, symmetric, nonnegative and suppose that supp. Let λ be an endpoint of the spectrum of μ considered as a convolver on ℓ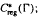2(Γ). Then λ − μ is in the left kernel of exactly one pure state of the reduced in particular, Paschke's conjecture holds for λ − μ.

The spherical functions of triangle buildings can be described in terms of certain two-dimensional orthogonal polynomials on Steiner's hypocycloid which are closely related to Hall-Littlewood polynomials. They lead to a one-parameter family of two-dimensional polynimial hypergroups. In this paper we investigate isotropic random walks on the vertex sets of triangle buildings in terms of their projections to these hypergroups. We present strong laws of large numbers, a central limit theorem, and a local limit theorem; all these results are well-known for homogeneous trees. Proofs are based on moment functions on hypergroups and on explicit expansions of the hypergroup characters in terms of certain two-dimensional Tchebychev polynimials.

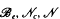Let and 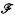denote respectively the variety of groups of exponent dividing 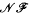e, the variety of nilpotent groups of class at most c, the class of nilpotent groups and the class of finite groups. It follows from a result due to Kargapolov and Čurkin and independently to Groves that in a variety not containing all metabelian groups, each polycyclic group G belongs to . We show that 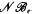G is in fact in , where c is an integer depending only on the variety. On the other hand, it is not always possible to find an integer e (depending only on the variety) such that G belongs to but we characterize the varieties in which that is possible. In this case, there exists a function 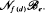f such that, if G is d-generated, then G ∈ So, when 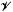e = 1, we obtain an extension of Zel'manov's result about the restricted Burnside problem (as one might expect, this result is used in our proof). 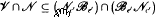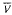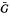Finally, we show that the class of locally nilpotent groups of a variety forms a variety if and only if for some integers c′, e′.

For each positive integer n let N2, n denote the variety of all groups which are nilpotent of class at most 2 and which have exponent dividing n. For positive integers m and n, let N2, mN2, n denote the variety of all groups which have a normal subgroup in N2, m with factor group in N2, n. It is shown that if G ∈N2, mN2, n, where m and n are coprime, then G has a finite basis for its identities.

Let Λ be an ordered abelian group. It is shown that groups in a certain class can have no non-trivial action of end type on a Λ-tree. A similar result is obtained for irreducible actions.

We provide an upper bound for the order of a nilpotent injector of a finite solvable group with Fitting subgroup of order n. We also show that the same bound is an upper bound for the number of conjugacy classes, provided that the k(G V)-conjecture holds for solvable G all primes dividing n.

Let G be a finite group that acts on a finite group V, and let p be a prime that does not divide the order of V. Then the p-parts of the orbit sizes are the same in the actions of G on the sets of conjugacy classes and irreducible characters of V. This result is derived as a consequence of some general theory relating orbits and chains of p-subgroups of a group.

Let S be a subset of a group G such that S−1 = S. Denote by gr (S) the subgroup of G generated by S, and by ls(g) the length of an element g ∈ gr(S) relative to the set S. Suppose that V is a finite subset of a free group F of countable rank such that the verbal subgroup V (F) is a proper subgroup of F. For an arbitrary group G, denote by (G) the set of values in G of all the words from the set V. In the present paper, for amalgamated products G = A *HB such that A ≠ H and the number of double cosets of B by H is at least three, the infiniteness of the set {ls(g) | g ∈ gr(S)}, where S = (G) ∪ (G)−1, is estabilished.

We investigate a locally full HNN extension of an inverse semigroup. A normal form theorem is obtained and applied to the word problem. We construct a tree and show that a maximal subgroup of a locally full HNN extension acts on the tree without inversion. Bass-Serre theory is employed to obtain a group presentation of the maximal subgroup as a fundamental group of a certain graph of groups associated with the D-structure of the original semigroup.

We show that if G is a finitely generated profinite group such that [x1, x2, …, xk] is Engel for any x1, x2, …, xk ∈ G, then γ(G) is locally nilpotent, and if [x1, x2, …, xk] has finite order for any x1, x2, …, xk ∈ G then, under some additional assumptions, γk(G) is locally finite.

A group G is locally graded if every finitely generated nontrivial subgroup of G has a nontrivial finite image. Let N (2, k)* denote the class of groups in which every infinite subset contains a pair of elements that generate a nilpotent subgroup of class at most k. We show that if G is a finitely generated locally graded N (2, k)*-group, then there is a positive integer c depending only on k such that G/Zc (G) is finite.

We provide a wedge decomposition of the homotopy type of the p-subgroup complex in the case of a finite solvable group G. In particular, this includes a new proof of the result of Quillen which says that this complex is contractible if and only if there is a non-trivial normal p-subgroup in G. We also provide reduction formulas for the G-module structure of the homology groups. Our results are obtained with diagram-methods by gluing the p-subgroup complex of G along the p-subgroup complex of = G/N for a normal p′-subgroup of G.

In this paper a necessary and sufficient condition will be given for groups to be ν-isologic, with respect to a given variety of groups ν. Its is also shown that every ν-isologism family of a group contains a ν-Hopfian group. Finally we show that if G is in the variety ν, then every ν-covering group of G is a Hopfian group.

The main result indicates that every finitely generated, residually finite, torsion-free, cohopfian group having on free Abelian subgroup of rank two is hyperhopfian. The argument relies on earlier work and ideas of Hirshon. As a corollary, fundamental groups of all closed hyperbolic manifolds are hyperhopfian.

Let K be an arbitrary field of characteristic 2, F a free group of countably infinite rank. We construct a finitely generated fully invariant subgroup U in F such that the relatively free group F/U satisfies the maximal condition on fully invariant subgroups but the group algebra K (F/U) does not satisfy the maximal condition on fully invariant ideals. This solves a problem posed by Plotkin and Vovsi. Using the developed techniques we also construct the first example of a non-finitely based (nilpotent of class 2)-by-(nilpotent of class 2) variety whose Abelian-by-(nilpotent of class at most 2) groups form a hereditarily finitely based subvariety.

An example is given of a finitely generated group G for which G ≅ G*cG, where C is infinite cyclic.

In previous work [2] calculations of subquadratic second order Dehn functions for various groups were carried out. In this paper we obtain estimates for upper and lower bounds of second order Dehn functions of HNN-extensions, and use these to exhibit an infinite number of different superquadratic second order Dehn functions. At the end of the paper several open questions concerning second order Dehn functions of groups are discussed.

The wreath product W = A ≀ T, where A ≠ 1, is of type F P2 if and only if T is finite and A is of type F P2.

This paper is concerned with the question of whether n-Engel groups are locally nilpotent. Although this seems unlikely in general, it is shown here that it is the case for the groups in a large class C including all residually soluble and residually finite groups (in fact all groups considered in traditional textbooks on group theory). This follows from the main result that there exist integers c(n), e(n) depending only on n, such that every finitely generated n-Engel group in the class C is both finite-of-exponent-e(n)–by–nilpotent-of-class≤c(n) and nilpotent-of-class≤c(n)–by–finite-of-exponent-e(n). Crucial in the proof is the fact that a finitely generated Engel group has finitely generated commutator subgroup.