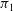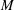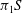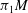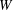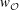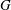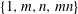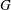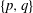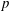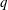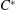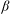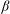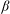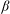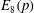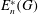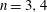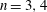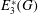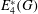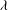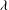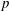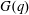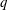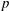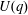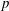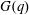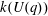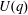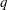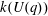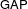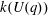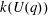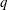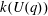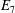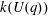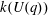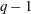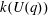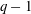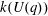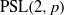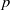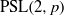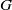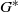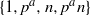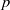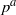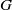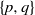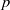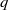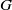Refine listing
Actions for selected content:
346 results in 20Exx
WORDS AND PRONILPOTENT SUBGROUPS IN PROFINITE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 29 September 2014, pp. 343-364
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Separability of embedded surfaces in 3-manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 9 / September 2014
- Published online by Cambridge University Press:
- 27 August 2014, pp. 1623-1630
- Print publication:
- September 2014
-
- Article
- Export citation
Minimal length elements of extended affine Weyl groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 11 / November 2014
- Published online by Cambridge University Press:
- 19 August 2014, pp. 1903-1927
- Print publication:
- November 2014
-
- Article
- Export citation
SOLVABILITY OF FINITE GROUPS WITH FOUR CONJUGACY CLASS SIZES OF CERTAIN ELEMENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 21 July 2014, pp. 250-256
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
TOPOLOGICAL FULL GROUPS OF
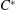 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}C^*$-ALGEBRAS ARISING FROM
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}C^*$-ALGEBRAS ARISING FROM 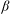 $\beta $-EXPANSIONS
$\beta $-EXPANSIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 17 July 2014, pp. 257-287
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
Rational rigidity for
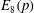 ${E}_{8}(p)$
${E}_{8}(p)$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 10 / October 2014
- Published online by Cambridge University Press:
- 17 July 2014, pp. 1679-1702
- Print publication:
- October 2014
-
- Article
- Export citation
ON NONINNER 2-AUTOMORPHISMS OF FINITE 2-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 29 May 2014, pp. 227-231
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
ON A PROBLEM OF P. HALL FOR ENGEL WORDS II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 13 May 2014, pp. 237-246
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
ON SOLUBILITY OF GROUPS WITH FEW NORMALISERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 12 May 2014, pp. 247-249
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
FREE GROUPS AND AUTOMORPHISM GROUPS OF INFINITE STRUCTURES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 17 April 2014, e8
-
- Article
-
- You have access
- Open access
- Export citation
Calculating conjugacy classes in Sylow
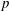 $p$ -subgroups of finite Chevalley groups of rank six and seven
$p$ -subgroups of finite Chevalley groups of rank six and seven
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 109-122
-
- Article
-
- You have access
- Export citation
Abstract simplicity of locally compact Kac–Moody groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 4 / April 2014
- Published online by Cambridge University Press:
- 10 March 2014, pp. 713-728
- Print publication:
- April 2014
-
- Article
- Export citation
Infinite presentability of groups and condensation
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 4 / October 2014
- Published online by Cambridge University Press:
- 02 January 2014, pp. 811-848
- Print publication:
- October 2014
-
- Article
- Export citation
The minimal generating sets of
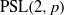 $\mathrm{PSL} (2, p)$ of size four
$\mathrm{PSL} (2, p)$ of size four
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 06 November 2013, pp. 419-423
-
- Article
-
- You have access
- Export citation
PROFINITE GROUPS WITH FINITE VIRTUAL LENGTH
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 18 July 2013, pp. 343-355
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
CONJUGACY CLASS SIZE CONDITIONS WHICH IMPLY SOLVABILITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 15 January 2013, pp. 297-300
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
A pair of characteristic subgroups for pushing-up. II
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 24 October 2012, pp. 71-133
-
- Article
-
- You have access
- Export citation
Finite p-solvable groups with three p-regular conjugacy class sizes
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 30 August 2012, pp. 371-386
-
- Article
-
- You have access
- Export citation
ON CENTRALISERS AND NORMALISERS FOR GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 02 August 2012, pp. 481-494
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
c-SECTIONS, SOLVABILITY AND LARGE SUBGROUPS OF FINITE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 2 / October 2012
- Published online by Cambridge University Press:
- 03 April 2012, pp. 291-302
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation