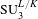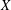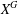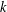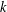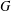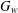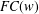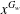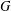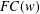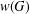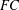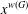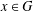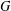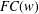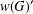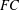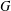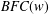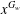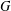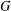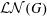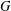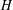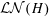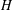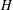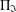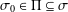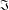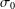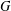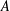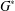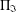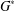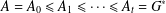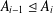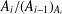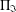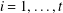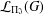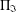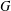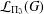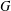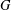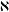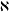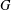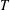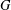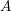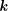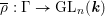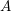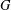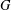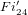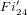Refine listing
Actions for selected content:
346 results in 20Exx
LOCALLY COMPACT WREATH PRODUCTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 15 August 2018, pp. 26-52
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
CHABAUTY LIMITS OF SIMPLE GROUPS ACTING ON TREES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 06 August 2018, pp. 1093-1120
- Print publication:
- July 2020
-
- Article
- Export citation
CHABAUTY LIMITS OF ALGEBRAIC GROUPS ACTING ON TREES THE QUASI-SPLIT CASE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 06 August 2018, pp. 1031-1091
- Print publication:
- July 2020
-
- Article
- Export citation
Maximal Subgroups and Irreducible Representations of Generalized Multi-Edge Spinal Groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 3 / August 2018
- Published online by Cambridge University Press:
- 17 April 2018, pp. 673-703
-
- Article
- Export citation
GROUPS OF FINITE NORMAL LENGTH
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 01 February 2018, pp. 229-239
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
Commutativity preserving extensions of groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 20 December 2017, pp. 575-592
- Print publication:
- June 2018
-
- Article
- Export citation
THE LOWER RANK OF DIRECT PRODUCTS OF HEREDITARILY JUST INFINITE GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 04 September 2017, pp. 225-230
- Print publication:
- January 2018
-
- Article
-
- You have access
- Export citation
ON GROUPS WITH FINITE CONJUGACY CLASSES IN A VERBAL SUBGROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 08 June 2017, pp. 429-437
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
LOCALLY NORMAL SUBGROUPS OF TOTALLY DISCONNECTED GROUPS. PART II: COMPACTLY GENERATED SIMPLE GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 22 May 2017, e12
-
- Article
-
- You have access
- Open access
- Export citation
LOCALLY NORMAL SUBGROUPS OF TOTALLY DISCONNECTED GROUPS. PART I: GENERAL THEORY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 22 May 2017, e11
-
- Article
-
- You have access
- Open access
- Export citation
ON THE LATTICE OF
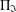 $\unicode[STIX]{x1D6F1}_{\mathfrak{I}}$ -SUBNORMAL SUBGROUPS OF A FINITE GROUP
$\unicode[STIX]{x1D6F1}_{\mathfrak{I}}$ -SUBNORMAL SUBGROUPS OF A FINITE GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 02 May 2017, pp. 233-244
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
LANDAU’S THEOREM, FIELDS OF VALUES FOR CHARACTERS, AND SOLVABLE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 23 December 2016, pp. 37-43
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
On Groups with Slow Intersection Growth
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 14 November 2016, pp. 387-390
-
- Article
- Export citation
A NOTE ON GROUPS WHOSE PROPER LARGE SUBGROUPS HAVE A TRANSITIVE NORMALITY RELATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 04 November 2016, pp. 38-47
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
SEMIPERMUTABILITY IN GENERALISED SOLUBLE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 02 November 2016, pp. 219-227
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
ON VARIETIES OF ABELIAN TOPOLOGICAL GROUPS WITH COPRODUCTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 19 October 2016, pp. 54-65
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
The inverse deformation problem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 8 / August 2016
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1725-1739
- Print publication:
- August 2016
-
- Article
- Export citation
L. G. KOVÁCS AND LINEAR GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 12 May 2016, pp. 55-62
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
NORMAL SUBGROUPS WHOSE CONJUGACY CLASS GRAPH HAS DIAMETER THREE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 266-272
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
Structure of the
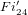 $Fi_{24}^{\prime }$ maximal
$Fi_{24}^{\prime }$ maximal  $2$ -local geometry point-line collinearity graph
$2$ -local geometry point-line collinearity graph
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 March 2016, pp. 105-154
-
- Article
-
- You have access
- Export citation