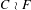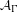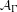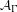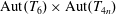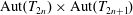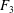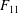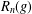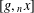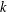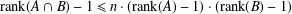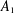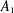Refine listing
Actions for selected content:
346 results in 20Exx
Simple groups and irreducible lattices in wreath products
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 07 February 2020, pp. 1502-1513
- Print publication:
- May 2021
-
- Article
- Export citation
Amenable uniformly recurrent subgroups and lattice embeddings
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 07 February 2020, pp. 1464-1501
- Print publication:
- May 2021
-
- Article
- Export citation
AXIOMATISABILITY OF THE CLASS OF MONOLITHIC GROUPS IN A VARIETY OF NILPOTENT GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 16 January 2020, pp. 67-76
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Revisiting Leighton’s theorem with the Haar measure
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 13 January 2020, pp. 615-623
- Print publication:
- May 2021
-
- Article
- Export citation
ON FINITE-BY-NILPOTENT GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 20 December 2019, pp. 54-58
- Print publication:
- January 2021
-
- Article
-
- You have access
- Export citation
On commensurability of right-angled Artin groups II: RAAGs defined by paths
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 12 December 2019, pp. 559-608
- Print publication:
- May 2021
-
- Article
- Export citation
Maximal hyperbolic towers and weight in the theory of free groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 18 November 2019, pp. 479-498
- Print publication:
- May 2021
-
- Article
- Export citation
Bounding the covolume of lattices in products
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 12 / December 2019
- Published online by Cambridge University Press:
- 11 October 2019, pp. 2296-2333
- Print publication:
- December 2019
-
- Article
- Export citation
New Simple Lattices in Products of Trees and their Projections
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 07 October 2019, pp. 1624-1690
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
Residually finite tubular groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 27 August 2019, pp. 2937-2951
- Print publication:
- December 2020
-
- Article
- Export citation
Quasi-Sturmian colorings on regular trees
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 09 August 2019, pp. 3403-3419
- Print publication:
- December 2020
-
- Article
- Export citation
Décomposition de Hodge pour l’homologie stable des groupes d’automorphismes des groupes libres
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 9 / September 2019
- Published online by Cambridge University Press:
- 07 August 2019, pp. 1794-1844
- Print publication:
- September 2019
-
- Article
- Export citation
On the residual and profinite closures of commensurated subgroups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 2 / September 2020
- Published online by Cambridge University Press:
- 30 July 2019, pp. 411-432
- Print publication:
- September 2020
-
- Article
- Export citation
Bounded Depth Ascending HNN Extensions and
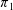 $\unicode[STIX]{x1D70B}_{1}$-Semistability at infinity
$\unicode[STIX]{x1D70B}_{1}$-Semistability at infinity
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 22 July 2019, pp. 1529-1550
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
RIGHT ENGEL-TYPE SUBGROUPS AND LENGTH PARAMETERS OF FINITE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 18 July 2019, pp. 340-350
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
INTERSECTIONS OF SUBGROUPS IN VIRTUALLY FREE GROUPS AND VIRTUALLY FREE PRODUCTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 18 July 2019, pp. 266-271
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
ON A LATTICE CHARACTERISATION OF FINITE SOLUBLE PST-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 10 July 2019, pp. 247-254
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
ON A PROBLEM OF PRAEGER AND SCHNEIDER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 27 May 2019, pp. 80-87
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
JSJ DECOMPOSITIONS OF DOUBLES OF FREE GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 02 May 2019, pp. 367-382
- Print publication:
- May 2020
-
- Article
-
- You have access
- Open access
- Export citation
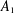 $A_{1}$-TYPE SUBGROUPS CONTAINING REGULAR UNIPOTENT ELEMENTS
$A_{1}$-TYPE SUBGROUPS CONTAINING REGULAR UNIPOTENT ELEMENTS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 24 April 2019, e12
-
- Article
-
- You have access
- Open access
- Export citation