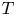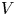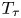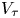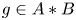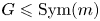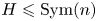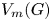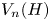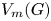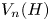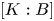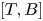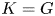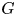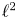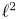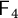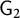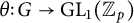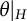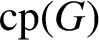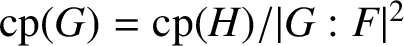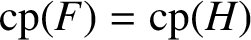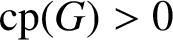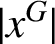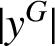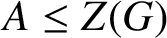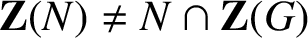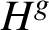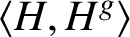Refine listing
Actions for selected content:
346 results in 20Exx
Irrational-slope versions of thompson's groups T and V
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 11 February 2022, pp. 244-262
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Thermodynamic metrics on outer space
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 3 / March 2023
- Published online by Cambridge University Press:
- 03 February 2022, pp. 729-793
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GROUPS WITH A GIVEN NUMBER OF NONPOWER SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 10 January 2022, pp. 315-319
- Print publication:
- October 2022
-
- Article
- Export citation
Weak amenability of free products of hyperbolic and amenable groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 06 January 2022, pp. 698-701
- Print publication:
- September 2022
-
- Article
- Export citation
Commutator length of powers in free products of groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 27 December 2021, pp. 102-119
-
- Article
- Export citation
Some embeddings between symmetric R. thompson groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 07 December 2021, pp. 1-18
-
- Article
- Export citation
On the commuting probability for subgroups of a finite group
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 18 November 2021, pp. 1551-1564
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Maximal subgroups of nontorsion Grigorchuk–Gupta–Sidki groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 02 November 2021, pp. 825-844
- Print publication:
- December 2022
-
- Article
- Export citation
The first $\ell ^{2}$
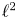 -betti number and groups acting on trees
-betti number and groups acting on trees
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 25 October 2021, pp. 916-923
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE PROFINITE COMPLETION OF A PROFINITE PROJECTIVE GROUP
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 23 August 2021, pp. 499-503
- Print publication:
- May 2022
-
- Article
- Export citation
Automorphisms and opposition in spherical buildings of exceptional type, I
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 05 July 2021, pp. 1517-1578
- Print publication:
- December 2022
-
- Article
- Export citation
Galois-theoretic features for 1-smooth pro-p groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 29 June 2021, pp. 525-541
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COMMUTING PROBABILITY OF COMPACT GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 24 June 2021, pp. 87-91
- Print publication:
- February 2022
-
- Article
- Export citation
ON GROUPS WHOSE SUBGROUPS ARE EITHER MODULAR OR CONTRANORMAL
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 18 June 2021, pp. 286-295
- Print publication:
- April 2022
-
- Article
- Export citation
ON THE REGULAR GRAPH RELATED TO THE G-CONJUGACY CLASSES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 12 May 2021, pp. 101-105
- Print publication:
- February 2022
-
- Article
- Export citation
GROUPS WITH MANY PRONORMAL SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 75-86
- Print publication:
- February 2022
-
- Article
-
- You have access
- Open access
- Export citation
EXTENDING RESULTS OF MORGAN AND PARKER ABOUT COMMUTING GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 92-100
- Print publication:
- February 2022
-
- Article
- Export citation
BEING CAYLEY AUTOMATIC IS CLOSED UNDER TAKING WREATH PRODUCT WITH VIRTUALLY CYCLIC GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 13 April 2021, pp. 464-474
- Print publication:
- December 2021
-
- Article
- Export citation
ON GRAEV’S THEOREM FOR FREE PRODUCTS OF HAUSDORFF TOPOLOGICAL GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 29 March 2021, pp. 475-483
- Print publication:
- December 2021
-
- Article
- Export citation
CONNECTED COMPONENTS IN THE INVARIABLY GENERATING GRAPH OF A FINITE GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 25 March 2021, pp. 453-463
- Print publication:
- December 2021
-
- Article
-
- You have access
- Open access
- Export citation