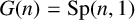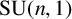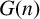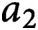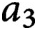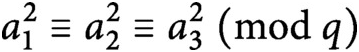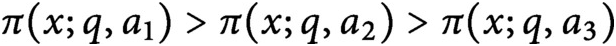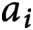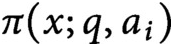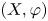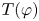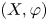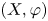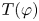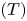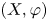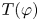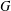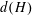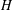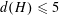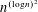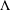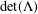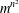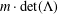Refine listing
Actions for selected content:
346 results in 20Exx
LOCAL COORDINATES FOR COMPLEX AND QUATERNIONIC HYPERBOLIC PAIRS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 04 March 2021, pp. 57-78
- Print publication:
- August 2022
-
- Article
- Export citation
STRONGLY BOUNDED LOCALLY INDICABLE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 19 February 2021, pp. 443-447
- Print publication:
- December 2021
-
- Article
- Export citation
ON THE AUTOMORPHISM GROUP OF THE UNIVERSAL HOMOGENEOUS MEET-TREE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 1508-1540
- Print publication:
- December 2021
-
- Article
- Export citation
THÉORIE DE BRUHAT-TITS POUR LES GROUPES QUASI-RÉDUCTIFS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 25 January 2021, pp. 1331-1362
- Print publication:
- July 2022
-
- Article
- Export citation
ON THE PRONORM OF A GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 20 January 2021, pp. 287-294
- Print publication:
- October 2021
-
- Article
- Export citation
On exceptional Lie geometries
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 11 January 2021, e2
-
- Article
-
- You have access
- Open access
- Export citation
Profinite invariants of arithmetic groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 13 November 2020, e54
-
- Article
-
- You have access
- Open access
- Export citation
Compact groups in which all elements have countable right Engel sinks
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 13 November 2020, pp. 1790-1814
- Print publication:
- December 2021
-
- Article
- Export citation
Densities in certain three-way prime number races
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 12 October 2020, pp. 232-265
- Print publication:
- February 2022
-
- Article
- Export citation
FURTHER REMARKS ON ELEMENTARY RADICALS AND ASSOCIATED FILTERS OF IDEALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 08 October 2020, pp. 450-460
- Print publication:
- June 2021
-
- Article
- Export citation
On solvable groups with one vanishing class size
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 14 September 2020, pp. 1467-1486
- Print publication:
- October 2021
-
- Article
- Export citation
A METRIC VERSION OF SCHLICHTING’S THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 07 September 2020, pp. 1607-1613
- Print publication:
- December 2020
-
- Article
- Export citation
On semidirectly closed non-aperiodic pseudovarieties of finite monoids
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 4 / November 2020
- Published online by Cambridge University Press:
- 24 August 2020, pp. 913-928
-
- Article
- Export citation
Groups of piecewise linear homeomorphisms of flows
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 05 October 2020, pp. 1595-1622
- Print publication:
- August 2020
-
- Article
- Export citation
ON EXTENSIONS OF PARTIAL ISOMORPHISMS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 20 July 2020, pp. 416-435
- Print publication:
- March 2022
-
- Article
- Export citation
GENERATING MAXIMAL SUBGROUPS OF FINITE ALMOST SIMPLE GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 30 June 2020, e32
-
- Article
-
- You have access
- Open access
- Export citation
BRANCH GROUPS, ORBIT GROWTH, AND SUBGROUP GROWTH TYPES FOR PRO-
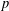 $p$ GROUPS
$p$ GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 26 May 2020, e10
-
- Article
-
- You have access
- Open access
- Export citation
DECOMPOSITION THEOREMS FOR AUTOMORPHISM GROUPS OF TREES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 20 May 2020, pp. 104-112
- Print publication:
- February 2021
-
- Article
- Export citation
CLASSIFICATION OF THE SUBLATTICES OF A LATTICE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 13 April 2020, pp. 50-61
- Print publication:
- February 2021
-
- Article
- Export citation
Orders on Trees and Free Products of Left-ordered Groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 31 March 2020, pp. 335-347
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation