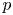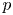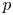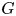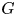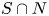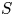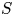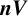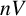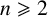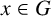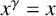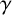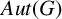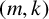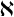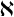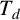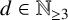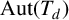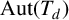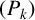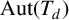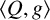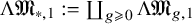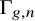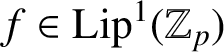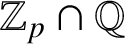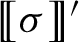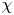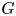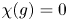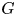Refine listing
Actions for selected content:
346 results in 20Exx
Conjugacy conditions for supersoluble complements of an abelian base and a fixed point result for non-coprime actions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 4 / November 2022
- Published online by Cambridge University Press:
- 24 November 2022, pp. 1075-1079
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PERMUTATION-BASED PRESENTATIONS FOR BRIN’S HIGHER-DIMENSIONAL THOMPSON GROUPS
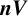 $\boldsymbol {nV}$
$\boldsymbol {nV}$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 15 November 2022, pp. 39-67
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE CENTRAL KERNEL OF A GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 13 October 2022, pp. 283-289
- Print publication:
- October 2023
-
- Article
- Export citation
GROUPS IN WHICH ALL LARGE SUBGROUPS HAVE BOUNDED NEAR DEFECT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 23 September 2022, pp. 456-463
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GROUPS ACTING ON TREES WITH PRESCRIBED LOCAL ACTION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 12 September 2022, pp. 240-288
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Kernels of localities
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 02 September 2022, e74
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Hanna Neumann conjecture for surface groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 9 / September 2022
- Published online by Cambridge University Press:
- 12 October 2022, pp. 1850-1877
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The equivalence between rational G-sheaves and rational G-Mackey functors for profinite G
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 30 August 2022, pp. 345-368
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the profinite rigidity of lattices in higher rank Lie groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 22 August 2022, pp. 369-384
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the dynamics of extensions of free-abelian times free groups endomorphisms to the completion
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 3 / August 2022
- Published online by Cambridge University Press:
- 12 August 2022, pp. 705-735
-
- Article
- Export citation
Maximal order Abelian subgroups of Coxeter groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 02 August 2022, pp. 114-120
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GROUPS WITH A LARGE PERMUTABLY EMBEDDED SUBGROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 13 July 2022, pp. 276-283
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SOME PRODUCTS OF SUBGROUPS AND VANISHING CONJUGACY CLASS SIZES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 13 July 2022, pp. 271-275
- Print publication:
- April 2023
-
- Article
- Export citation
MODEL THEORY OF GALOIS ACTIONS OF TORSION ABELIAN GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 30 June 2022, pp. 2943-2985
- Print publication:
- November 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Parametrised moduli spaces of surfaces as infinite loop spaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 09 June 2022, e39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CAYLEY–ABELS GRAPHS AND INVARIANTS OF TOTALLY DISCONNECTED, LOCALLY COMPACT GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 114 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 13 April 2022, pp. 145-177
- Print publication:
- April 2023
-
- Article
- Export citation
SOLENOIDAL MAPS, AUTOMATIC SEQUENCES, VAN DER PUT SERIES, AND MEALY AUTOMATA
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 114 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 06 April 2022, pp. 78-109
- Print publication:
- February 2023
-
- Article
- Export citation
Topological full groups of minimal subshifts and quantifying local embeddings into finite groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 05 April 2022, pp. 1492-1510
- Print publication:
- May 2023
-
- Article
- Export citation
Overgroups of regular unipotent elements in reductive groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 24 February 2022, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On finite groups with exactly one vanishing conjugacy class size
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 15 February 2022, pp. 344-368
- Print publication:
- February 2023
-
- Article
- Export citation