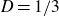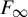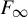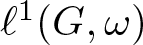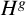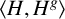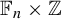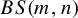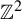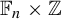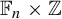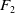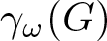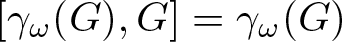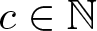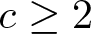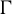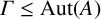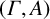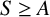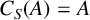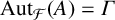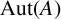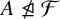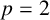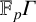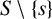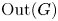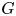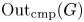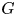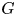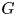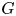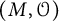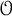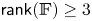Refine listing
Actions for selected content:
346 results in 20Exx
Continuum of allosteric actions for non-amenable surface groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 19 July 2023, pp. 1581-1596
- Print publication:
- June 2024
-
- Article
- Export citation
SELF-DIVISIBLE ULTRAFILTERS AND CONGRUENCES IN
 $\beta {\mathbb {Z}}$
$\beta {\mathbb {Z}}$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 17 July 2023, pp. 1180-1197
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Prime divisors and the number of conjugacy classes of finite groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 10 July 2023, pp. 1-16
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finitely presented left orderable monsters
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 06 July 2023, pp. 1367-1378
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Dales–Żelazko conjecture for Beurling algebras on discrete groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 03 July 2023, pp. 613-624
-
- Article
- Export citation
LOCALLY FINITE SIMPLE GROUPS WHOSE NONNILPOTENT SUBGROUPS ARE PRONORMAL
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 29 June 2023, pp. 512-521
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Groups of small period growth
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 27 June 2023, pp. 625-641
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Strongly aperiodic SFTs on generalized Baumslag–Solitar groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 20 June 2023, pp. 1209-1238
- Print publication:
- May 2024
-
- Article
- Export citation
Continuously many quasi-isometry classes of residually finite groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 19 June 2023, pp. 569-572
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on virtual duality and automorphism groups of right-angled Artin groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 19 June 2023, pp. 573-581
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Baumslag–Solitar groups and residual nilpotence
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 16 June 2023, pp. 532-547
-
- Article
- Export citation
Co-spectral radius of intersections
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 17 April 2023, pp. 509-523
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NONREALIZABILITY OF CERTAIN REPRESENTATIONS IN FUSION SYSTEMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 11 April 2023, pp. 257-288
- Print publication:
- April 2024
-
- Article
- Export citation
Phase transitions for non-singular Bernoulli actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 11 April 2023, pp. 353-382
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FINITE GROUPS WITH INDEPENDENT GENERATING SETS OF ONLY TWO SIZES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 23 February 2023, pp. 449-458
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On automorphisms and splittings of special groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 10 February 2023, pp. 232-305
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A parametrization of sheets of conjugacy classes in bad characteristic
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 26 January 2023, pp. 976-983
- Print publication:
- September 2023
-
- Article
- Export citation
Conjugacy growth in the higher Heisenberg groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue S1 / May 2023
- Published online by Cambridge University Press:
- 23 January 2023, pp. S148-S169
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON SUBNORMAL SUBGROUPS IN DIVISION RINGS CONTAINING SOLVABLE SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 11 January 2023, pp. 422-427
- Print publication:
- December 2023
-
- Article
- Export citation
Relative hyperbolicity of free-by-cyclic extensions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 30 January 2023, pp. 153-183
- Print publication:
- January 2023
-
- Article
- Export citation