Refine listing
Actions for selected content:
346 results in 20Exx
Varieties of groups and isologisms
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 46 / Issue 1 / February 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 22-60
- Print publication:
- February 1989
-
- Article
-
- You have access
- Export citation
Subnormal subgroups in direct products of groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 42 / Issue 2 / April 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 147-172
- Print publication:
- April 1987
-
- Article
-
- You have access
- Export citation
CLT groups and wreath products
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 42 / Issue 2 / April 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 183-195
- Print publication:
- April 1987
-
- Article
-
- You have access
- Export citation
Free products of topological groups with a closed subgroup amalgamated
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 40 / Issue 3 / June 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 414-420
- Print publication:
- June 1986
-
- Article
-
- You have access
- Export citation
Automorphism orbits of finite groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 40 / Issue 2 / April 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 253-260
- Print publication:
- April 1986
-
- Article
-
- You have access
- Export citation
Special series of unitary representations of groups acting on homogeneous trees
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 40 / Issue 1 / February 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 83-88
- Print publication:
- February 1986
-
- Article
-
- You have access
- Export citation
Automorphisms of nilpotent groups of class two with small rank
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 1 / August 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 121-131
- Print publication:
- August 1985
-
- Article
-
- You have access
- Export citation
The structure of a group of permutation polynomials
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 2 / April 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 164-170
- Print publication:
- April 1985
-
- Article
-
- You have access
- Export citation
Some examples of finiteness conditions in centre-by-metabelian groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 2 / April 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 171-174
- Print publication:
- April 1985
-
- Article
-
- You have access
- Export citation
On the lower central factors of free centre-by-metabelian groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 1 / February 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 65-75
- Print publication:
- February 1985
-
- Article
-
- You have access
- Export citation
On certain varieties of groups which are central extensions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 3 / December 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 366-390
- Print publication:
- December 1984
-
- Article
-
- You have access
- Export citation
A conjecture of Lennox and Wiegold concerning supersoluble groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 35 / Issue 2 / October 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 218-220
- Print publication:
- October 1983
-
- Article
-
- You have access
- Export citation
Varieties of nilpotent groups of class four (I)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 35 / Issue 1 / August 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 59-73
- Print publication:
- August 1983
-
- Article
-
- You have access
- Export citation
Varieties of nilpotent groups of class four (III)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 35 / Issue 1 / August 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 109-122
- Print publication:
- August 1983
-
- Article
-
- You have access
- Export citation
Varieties of nilpotent groups of class four (II)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 35 / Issue 1 / August 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 74-108
- Print publication:
- August 1983
-
- Article
-
- You have access
- Export citation
Hall-closure and products of Fitting classes
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 32 / Issue 2 / April 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 145-164
- Print publication:
- April 1982
-
- Article
-
- You have access
- Export citation
Finite varieties and groups with Sylow p-subgroups of low class
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 4 / December 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 464-469
- Print publication:
- December 1981
-
- Article
-
- You have access
- Export citation
Extensions of a problem of Paul Erdös on groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 4 / December 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 459-463
- Print publication:
- December 1981
-
- Article
-
- You have access
- Export citation
The solutions to two problems on permutational products
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 4 / December 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 390-394
- Print publication:
- December 1981
-
- Article
-
- You have access
- Export citation
On the Schur-Baer property
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 3 / October 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 343-361
- Print publication:
- October 1981
-
- Article
-
- You have access
- Export citation
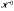 be the space of functions on the Poission boundary ω, of zero mean on ω. When
be the space of functions on the Poission boundary ω, of zero mean on ω. When 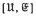 of all groups which are central extensions by groups in
of all groups which are central extensions by groups in 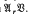 . Here
. Here 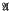 , is the variety of abelian groups of exponent dividing
, is the variety of abelian groups of exponent dividing 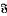 , is said to be Hall π-closed (where π is a set of primes) if whenever
, is said to be Hall π-closed (where π is a set of primes) if whenever 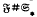 (where
(where 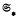 denotes the so-called smallest normal Fitting class), subject to a restriction connecting π with the characteristic of
denotes the so-called smallest normal Fitting class), subject to a restriction connecting π with the characteristic of 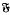 . We also characterise those Fitting classes
. We also characterise those Fitting classes 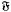 (respectively,
(respectively, 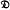 ) such that
) such that 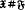 (respectively,
(respectively, 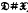 ) is Hall π-closed for all Fitting classes
) is Hall π-closed for all Fitting classes 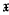 . In each case, part of the proof uses a concrete group construction. As a bonus, one of these construction also yields a “cancellation result” for certain products of Fitting classes.
. In each case, part of the proof uses a concrete group construction. As a bonus, one of these construction also yields a “cancellation result” for certain products of Fitting classes.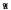 = (
= (