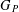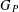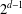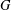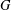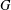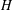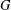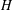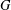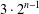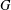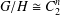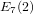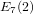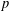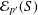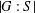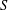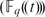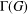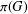Refine listing
Actions for selected content:
346 results in 20Exx
THE FIRST-ORDER THEORY OF BRANCH GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 10 February 2016, pp. 150-158
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
GROUPS OF INFINITE RANK WITH NORMALITY CONDITIONS ON SUBGROUPS WITH SMALL NORMAL CLOSURE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 11 November 2015, pp. 48-53
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
FINITELY CONSTRAINED GROUPS OF MAXIMAL HAUSDORFF DIMENSION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 11 November 2015, pp. 108-123
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
THE CONTRIBUTION OF L. G. KOVÁCS TO THE THEORY OF PERMUTATION GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 05 November 2015, pp. 20-33
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
ON GENERALISED FC-GROUPS IN WHICH NORMALITY IS A TRANSITIVE RELATION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 29 October 2015, pp. 192-198
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
TRANSVERSALS AS GENERATING SETS IN FINITELY GENERATED GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 19 August 2015, pp. 47-60
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
A LOCALISABLE CLASS OF PRIMITIVE IDEALS OF UNIFORM NILPOTENT IWASAWA ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 1-15
- Print publication:
- January 2016
-
- Article
-
- You have access
- Export citation
Virtual geometricity is rare
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 July 2015, pp. 444-455
-
- Article
-
- You have access
- Export citation
THE WORK OF L. G. KOVÁCS ON REPRESENTATION THEORY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 16 June 2015, pp. 34-42
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
Inversion is Possible in Groups with no Periodic Automorphisms
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 05 June 2015, pp. 11-16
-
- Article
- Export citation
CAUCHY–DAVENPORT TYPE THEOREMS FOR SEMIGROUPS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 22 May 2015, pp. 1-12
- Print publication:
- 2016
-
- Article
- Export citation
L. G. KOVÁCS AND VARIETIES OF GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 13 May 2015, pp. 43-54
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
AN APPROACH TO CAPABLE GROUPS AND SCHUR’S THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 05 May 2015, pp. 52-56
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
The maximal subgroups of
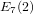 $E_{7}(2)$
$E_{7}(2)$
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 April 2015, pp. 323-371
-
- Article
-
- You have access
- Export citation
ON GROUPS PRESENTED BY MONADIC REWRITING SYSTEMS WITH GENERATORS OF FINITE ORDER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 06 March 2015, pp. 426-434
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
THE NUMBER OF PROFINITE GROUPS WITH A SPECIFIED SYLOW SUBGROUP
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 19 January 2015, pp. 108-127
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
COCOMPACT LATTICES ON Ãn BUILDINGS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 17 December 2014, pp. 241-262
- Print publication:
- May 2015
-
- Article
-
- You have access
- Export citation
EMBEDDABILITY OF GENERALISED WREATH PRODUCTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 15 December 2014, pp. 250-263
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
Random groups and nonarchimedean lattices
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 16 October 2014, e26
-
- Article
-
- You have access
- Open access
- Export citation
ON THE PRIME GRAPH OF SIMPLE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 08 October 2014, pp. 227-240
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation