Refine listing
Actions for selected content:
346 results in 20Exx
ON A GRAPH RELATED TO THE MAXIMAL SUBGROUPS OF A GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 14 January 2010, pp. 317-328
- Print publication:
- April 2010
-
- Article
-
- You have access
- Export citation
Simplicial cohomology of augmentation ideals in l1(G)
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 12 January 2010, pp. 97-109
-
- Article
-
- You have access
- Export citation
GROUPS WITH ABELIAN SYLOW SUBGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 16 December 2009, pp. 43-47
- Print publication:
- February 2010
-
- Article
-
- You have access
- Export citation
Multiplicative Invariants and the Finite Co-Hopfian Property
- Part of
-
- Journal:
- Mathematika / Volume 55 / Issue 1-2 / December 2009
- Published online by Cambridge University Press:
- 21 December 2009, pp. 115-127
- Print publication:
- December 2009
-
- Article
- Export citation
Harmonic and equianharmonic equations in the Grothendieck–Teichmüller group. III
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 11 August 2009, pp. 431-448
- Print publication:
- April 2010
-
- Article
- Export citation
FINITE GROUPS WITH TWO p-REGULAR CONJUGACY CLASS LENGTHS II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 3 / June 2009
- Published online by Cambridge University Press:
- 17 April 2009, pp. 419-425
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
AUTOMORPHISM GROUPS OF THE IMPRIMITIVE COMPLEX REFLECTION GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 01 February 2009, pp. 123-138
- Print publication:
- February 2009
-
- Article
-
- You have access
- Export citation
VARIETIES OF ABELIAN TOPOLOGICAL GROUPS AND SCATTERED SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 487-495
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
CONJUGACY CLASS SIZES IN FINITE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 85 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 251-255
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
Genericity, generosity, and tori
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 7 / Issue 4 / October 2008
- Published online by Cambridge University Press:
- 07 October 2008, pp. 705-722
- Print publication:
- October 2008
-
- Article
- Export citation
De non ordinaria recognitione PSL2
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 7 / Issue 4 / October 2008
- Published online by Cambridge University Press:
- 07 October 2008, pp. 723-734
- Print publication:
- October 2008
-
- Article
- Export citation
THE DENSITY OF SUBGROUP INDICES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 85 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 257-267
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
SCHREIER CONDITIONS ON CHIEF FACTORS AND RESIDUALS OF SOLVABLE-LIKE GROUP FORMATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 97-106
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
RIGIDITY OF GRAPH PRODUCTS OF ABELIAN GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 187-196
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
COMMUTATIVITY DEGREES OF WREATH PRODUCTS OF FINITE ABELIAN GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 31-36
- Print publication:
- February 2008
-
- Article
-
- You have access
- Export citation
OUTER AUTOMORPHISM GROUPS OF CERTAIN TREE PRODUCTS OF ABELIAN GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 9-20
- Print publication:
- February 2008
-
- Article
-
- You have access
- Export citation
Rate of escape of random walks on free products
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 1 / August 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 31-54
- Print publication:
- August 2007
-
- Article
-
- You have access
- Export citation
The palindromic width of a free product of groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 2 / October 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 199-208
- Print publication:
- October 2006
-
- Article
-
- You have access
- Export citation
Elements of minimal breadth in finite p-groups and lie algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 2 / October 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 209-214
- Print publication:
- October 2006
-
- Article
-
- You have access
- Export citation
The commutator subgroup and Schur multiplier of a pair of finite p-groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 1 / August 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-10
- Print publication:
- August 2006
-
- Article
-
- You have access
- Export citation
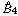 . A consequence is to represent a matrix specialization of the ‘equianharmonic’ parameter in terms of special values of the adelic beta function introduced and studied by Anderson and Ihara.
. A consequence is to represent a matrix specialization of the ‘equianharmonic’ parameter in terms of special values of the adelic beta function introduced and studied by Anderson and Ihara.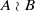 of finite Abelian groups
of finite Abelian groups 