Refine listing
Actions for selected content:
346 results in 20Exx
SOME GROUPS WITH COMPUTABLE CHERMAK–DELGADO LATTICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 1 / August 2012
- Published online by Cambridge University Press:
- 27 March 2012, pp. 29-40
- Print publication:
- August 2012
-
- Article
-
- You have access
- Export citation
Quantifying residual finiteness of arithmetic groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 19 March 2012, pp. 907-920
- Print publication:
- May 2012
-
- Article
-
- You have access
- Export citation
CONJUGACY CLASS SIZES OF CERTAIN DIRECT PRODUCTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 27 February 2012, pp. 217-231
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
GENERALISING QUASINORMAL SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 1 / August 2012
- Published online by Cambridge University Press:
- 23 February 2012, pp. 1-10
- Print publication:
- August 2012
-
- Article
-
- You have access
- Export citation
COHOMOLOGY AND PROFINITE TOPOLOGIES FOR SOLVABLE GROUPS OF FINITE RANK
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 2 / October 2012
- Published online by Cambridge University Press:
- 16 February 2012, pp. 254-265
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
ON GROUPS WITH A FINITE NUMBER OF NORMALISERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 14 February 2012, pp. 416-423
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
Bruhat–Tits theory from Berkovich's point of view. II Satake compactifications of buildings
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 11 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 13 December 2011, pp. 421-465
- Print publication:
- April 2012
-
- Article
- Export citation
Kähler groups, real hyperbolic spaces and the Cremona group. With an appendix by Serge Cantat
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 30 November 2011, pp. 153-184
- Print publication:
- January 2012
-
- Article
-
- You have access
- Export citation
ITÔ’S THEOREM ON GROUPS WITH TWO CLASS SIZES REVISITED
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 19 October 2011, pp. 476-481
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
Actions of higher-rank lattices on free groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 29 July 2011, pp. 1573-1580
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
Alternating units as free factors in the group of units of integral group rings
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 3 / October 2011
- Published online by Cambridge University Press:
- 14 June 2011, pp. 695-709
-
- Article
-
- You have access
- Export citation
ON VERBAL SUBGROUPS IN RESIDUALLY FINITE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 1 / August 2011
- Published online by Cambridge University Press:
- 10 June 2011, pp. 159-170
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
EXOTIC LEFT-ORDERINGS OF THE FREE GROUPS FROM THE DEHORNOY ORDERING
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 1 / August 2011
- Published online by Cambridge University Press:
- 01 April 2011, pp. 103-110
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
Growth in Baumslag–Solitar groups I: subgroups and rationality
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 14 / 2011
- Published online by Cambridge University Press:
- 01 February 2011, pp. 34-71
-
- Article
-
- You have access
- Export citation
Surface groups within Baumslag doubles
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 19 January 2011, pp. 91-97
-
- Article
-
- You have access
- Export citation
POSITIVE LAWS ON LARGE SETS OF GENERATORS: COUNTEREXAMPLES FOR INFINITELY GENERATED GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 3 / December 2010
- Published online by Cambridge University Press:
- 01 April 2011, pp. 289-296
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
PRONORMALITY IN GENERALIZED FC-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 14 September 2010, pp. 220-230
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
FINITE GROUPS WHOSE NONCENTRAL COMMUTING ELEMENTS HAVE CENTRALIZERS OF EQUAL SIZE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 07 July 2010, pp. 293-304
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
Constructing maximal subgroups of orthogonal groups
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 May 2010, pp. 164-191
-
- Article
-
- You have access
- Export citation
ON FINITE p-GROUPS WITH SUBGROUPS OF BREADTH 1
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 1 / August 2010
- Published online by Cambridge University Press:
- 12 April 2010, pp. 84-98
- Print publication:
- August 2010
-
- Article
-
- You have access
- Export citation
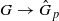 induces an isomorphism
induces an isomorphism 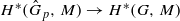 for any discrete
for any discrete 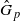 -module
-module 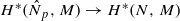 is an isomorphism for any discrete
is an isomorphism for any discrete 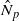 -module
-module 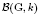 of a connected and reductive linear algebraic group G over a non-Archimedean field
of a connected and reductive linear algebraic group G over a non-Archimedean field 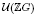 , the group of units of ℤ
, the group of units of ℤ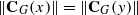 . Applying results of Schmidt [‘Zentralisatorverbände endlicher Gruppen’,
. Applying results of Schmidt [‘Zentralisatorverbände endlicher Gruppen’, 