Refine listing
Actions for selected content:
70 results in 44Axx
A family of strongly singular operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 67 / Issue 1 / August 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 58-84
- Print publication:
- August 1999
-
- Article
-
- You have access
- Export citation
Direct and converse inequalities for positive linear operators on the positive semi-axis
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 1 / February 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 90-103
- Print publication:
- February 1999
-
- Article
-
- You have access
- Export citation
Radon transform on affine buildings of rank three
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 1 / February 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 66-89
- Print publication:
- February 1999
-
- Article
-
- You have access
- Export citation
Computer Tomography and Quantum Mechanics
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 595-606
- Print publication:
- September 1997
-
- Article
- Export citation
Approximating gamma distributions by normalized negative binomial distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 391-400
- Print publication:
- June 1994
-
- Article
- Export citation
The distribution of apparent occupancy times in a two-state Markov process in which brief events cannot be detected
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 288-301
- Print publication:
- June 1992
-
- Article
- Export citation
On certain methods of solving a class of integral equations of Fredholm type
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 52 / Issue 1 / February 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-10
- Print publication:
- February 1992
-
- Article
-
- You have access
- Export citation
Sharp function estimates for fractional integrals and related operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 1 / August 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 129-137
- Print publication:
- August 1990
-
- Article
-
- You have access
- Export citation
A Property of completely monotonic functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 42 / Issue 2 / April 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 143-146
- Print publication:
- April 1987
-
- Article
-
- You have access
- Export citation
Multidimensional Volterra integral equations of convolution type
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 27 / Issue 3 / May 1979
- Published online by Cambridge University Press:
- 09 April 2009, pp. 305-312
- Print publication:
- May 1979
-
- Article
-
- You have access
- Export citation
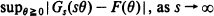 . In particular, we show that the exact order of uniform convergence is
. In particular, we show that the exact order of uniform convergence is 