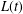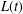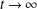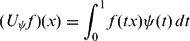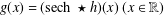Refine listing
Actions for selected content:
70 results in 44Axx
LARGE DEVIATIONS FOR THE LONGEST GAP IN POISSON PROCESSES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 16 October 2019, pp. 146-156
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
A support theorem for the X-ray transform on manifolds with plane covers
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 1 / July 2020
- Published online by Cambridge University Press:
- 25 April 2019, pp. 149-158
- Print publication:
- July 2020
-
- Article
- Export citation
Estimates for the order of Nevanlinna matrices and a Berezanskii-type theorem
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 26 January 2019, pp. 1637-1661
- Print publication:
- December 2019
-
- Article
- Export citation
FOURIER-TYPE TRANSFORMS ON REARRANGEMENT-INVARIANT QUASI-BANACH FUNCTION SPACES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 20 June 2018, pp. 231-248
- Print publication:
- January 2019
-
- Article
-
- You have access
- Export citation
GENERALIZED HARDY–CESÀRO OPERATORS BETWEEN WEIGHTED SPACES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 28 January 2018, pp. 13-24
- Print publication:
- January 2019
-
- Article
-
- You have access
- Export citation
On sequences of expected maxima and expected ranges
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 30 November 2017, pp. 1144-1166
- Print publication:
- December 2017
-
- Article
- Export citation
PRICING PERPETUAL TIMER OPTION UNDER THE STOCHASTIC VOLATILITY MODEL OF HULL–WHITE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 3-4 / April 2017
- Published online by Cambridge University Press:
- 16 May 2017, pp. 406-416
-
- Article
-
- You have access
- Export citation
ON THE DETERMINATION OF STAR BODIES FROM THEIR HALF-SECTIONS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 462-468
- Print publication:
- 2017
-
- Article
- Export citation
CONVERGENCE IN RELAXATION SPECTRUM RECOVERY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 02 November 2016, pp. 121-132
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
Laplace transform asymptotics and large deviation principles for longest success runs in Bernoulli trials
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 24 October 2016, pp. 747-764
- Print publication:
- September 2016
-
- Article
- Export citation
Approximating the Laplace transform of the sum of dependent lognormals
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue A / July 2016
- Published online by Cambridge University Press:
- 25 July 2016, pp. 203-215
- Print publication:
- July 2016
-
- Article
- Export citation
A SHARP VERSION OF BONSALL’S INEQUALITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 19 August 2015, pp. 397-404
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
A Two-Sided Laplace Inversion Algorithm with Computable Error Bounds and its Applications in Financial Engineering
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 3 / September 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 766-789
- Print publication:
- September 2014
-
- Article
-
- You have access
- Export citation
ON THE RANKIN–SELBERG ZETA FUNCTION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 19 September 2012, pp. 101-113
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
Laguerre semigroup and Dunkl operators
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 4 / July 2012
- Published online by Cambridge University Press:
- 18 May 2012, pp. 1265-1336
- Print publication:
- July 2012
-
- Article
-
- You have access
- Export citation
Pricing and Hedging of Quantile Options in a Flexible Jump Diffusion Model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 3 / September 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 637-656
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
Pricing the Zero-Coupon Bond and its Fair Premium Under a Structural Credit Risk Model with Jumps
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 404-419
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
New Limiting Distributions for Bellman-Harris Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 313-321
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
The Logarithmic Skew-Normal Distributions are Moment-Indeterminate
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 3 / September 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 909-916
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
A Two-Step Branching Splitting Model Under Cost Constraint for Rare Event Analysis
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 429-452
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation