Refine listing
Actions for selected content:
70 results in 44Axx
Analytic functions associated with strong Hamburger moment problems
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 02 February 2009, pp. 181-187
-
- Article
-
- You have access
- Export citation
Laplace Transforms of Probability Distributions and Their Inversions are Easy on Logarithmic Scales
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 2 / June 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 531-541
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
THE COMPLEX INVERSION FORMULA REVISITED
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 73-83
- Print publication:
- February 2008
-
- Article
-
- You have access
- Export citation
Resolution in hölder spaces of an elliptic problem in an unbounded domain
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 3 / December 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 387-404
- Print publication:
- December 2006
-
- Article
-
- You have access
- Export citation
The Lower Dimensional Busemann-Petty Problem with Weights
- Part of
-
- Journal:
- Mathematika / Volume 53 / Issue 2 / December 2006
- Published online by Cambridge University Press:
- 21 December 2009, pp. 235-245
- Print publication:
- December 2006
-
- Article
- Export citation
Poisson random balls: self-similarity and X-ray images
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 4 / December 2006
- Published online by Cambridge University Press:
- 08 September 2016, pp. 853-872
- Print publication:
- December 2006
-
- Article
-
- You have access
- Export citation
The diffusion of Radon shape
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 320-335
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
Sharp reliability bounds for the ℒ-like distributions, a class in which ageing is based on Laplace transform inequalities
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 4 / December 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1204-1208
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
The moment problem for some Wiener functionals: corrections to previous proofs (with an appendix by H. L. Pedersen)
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 3 / September 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 851-860
- Print publication:
- September 2005
-
- Article
-
- You have access
- Export citation
Negative definite and Schoenberg functions on commutative hypergroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 1 / August 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 25-37
- Print publication:
- August 2005
-
- Article
-
- You have access
- Export citation
On the distribution of the search cost for the move-to-front rule with random weights
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 1 / March 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 250-262
- Print publication:
- March 2004
-
- Article
- Export citation
Correction to a paper by A. G. Pakes
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 1 / February 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 67-74
- Print publication:
- February 2004
-
- Article
-
- You have access
- Export citation
Stieltjes classes for moment-indeterminate probability distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue A / 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 281-294
- Print publication:
- 2004
-
- Article
- Export citation
On the moment problem for random sums
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 3 / September 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 797-802
- Print publication:
- September 2003
-
- Article
- Export citation
First passage times of a jump diffusion process
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 2 / June 2003
- Published online by Cambridge University Press:
- 22 February 2016, pp. 504-531
- Print publication:
- June 2003
-
- Article
- Export citation
On the moment determinacy of the distributions of compound geometric sums
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 39 / Issue 3 / September 2002
- Published online by Cambridge University Press:
- 14 July 2016, pp. 545-554
- Print publication:
- September 2002
-
- Article
- Export citation
Moment sequences and backward extensions of subnormal weighted shifts
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 1 / August 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 27-36
- Print publication:
- August 2002
-
- Article
-
- You have access
- Export citation
A note on the ℒ-class of life distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 39 / Issue 1 / March 2002
- Published online by Cambridge University Press:
- 14 July 2016, pp. 11-19
- Print publication:
- March 2002
-
- Article
- Export citation
On the rose of intersections of stationary flat processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 33 / Issue 3 / September 2001
- Published online by Cambridge University Press:
- 01 July 2016, pp. 584-599
- Print publication:
- September 2001
-
- Article
- Export citation
Remarks on converse Carleman and Krein criteria for the classical moment problem
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 1 / August 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 81-104
- Print publication:
- August 2001
-
- Article
-
- You have access
- Export citation
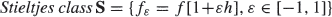 , where
, where 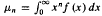 satisfying
satisfying 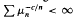 implies that
implies that