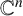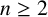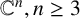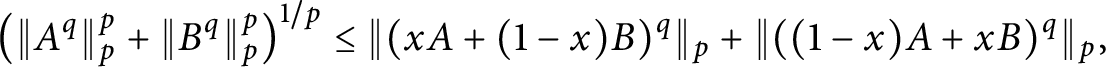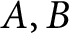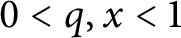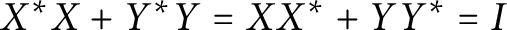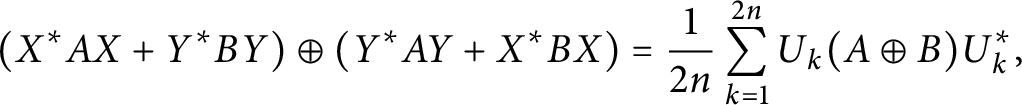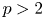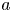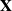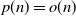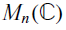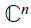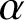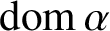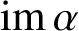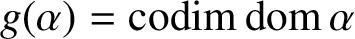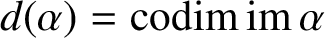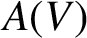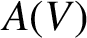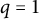Refine listing
Actions for selected content:
258 results in 15xxx
MINIMALLY TRANSITIVE FAMILIES OF SUBSPACES OF
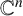 $\mathbb {C}^n$
$\mathbb {C}^n$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 20 January 2022, pp. 70-82
- Print publication:
- August 2022
-
- Article
- Export citation
Matrix inequalities and majorizations around Hermite–Hadamard’s inequality
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 10 January 2022, pp. 943-952
- Print publication:
- December 2022
-
- Article
- Export citation
Graded identities for algebras with elementary gradings over an infinite field
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 10 January 2022, pp. 146-166
-
- Article
- Export citation
ON THE NONNEGATIVITY OF THE DIRICHLET ENERGY OF A WEIGHTED GRAPH
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 17 December 2021, pp. 301-305
- Print publication:
- October 2022
-
- Article
- Export citation
Large-deviation asymptotics of condition numbers of random matrices
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 1114-1130
- Print publication:
- December 2021
-
- Article
- Export citation
AN EIGENVALUE CHARACTERISATION OF THE DUAL EDM CONE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 18 November 2021, pp. 67-69
- Print publication:
- August 2022
-
- Article
- Export citation
A refined nc Oka–Weil theorem
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 02 November 2021, pp. 218-224
- Print publication:
- March 2023
-
- Article
- Export citation
Commutativity via spectra of exponentials
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 02 November 2021, pp. 815-824
- Print publication:
- December 2022
-
- Article
- Export citation
ALMOST DISJOINT AND MAD FAMILIES IN VECTOR SPACES AND CHOICE PRINCIPLES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 29 October 2021, pp. 1093-1110
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Non-negative integral matrices with given spectral radius and controlled dimension
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 10 / October 2022
- Published online by Cambridge University Press:
- 21 September 2021, pp. 3246-3269
- Print publication:
- October 2022
-
- Article
- Export citation
Hilbert’s 17th problem in free skew fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 06 September 2021, e61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spectral gap in random bipartite biregular graphs and applications
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 23 July 2021, pp. 229-267
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
STRUCTURED SINGULAR VALUES OF SOME GENERALISED STOCHASTIC MATRICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 09 July 2021, pp. 58-67
- Print publication:
- February 2022
-
- Article
- Export citation
HERMITIANS IN MATRIX ALGEBRAS WITH OPERATOR NORM – II
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 10 June 2021, pp. 376-396
- Print publication:
- May 2022
-
- Article
- Export citation
HANKEL DETERMINANTS OF FACTORIAL FRACTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 07 June 2021, pp. 46-57
- Print publication:
- February 2022
-
- Article
- Export citation
Spectral distribution of symmetrized circulant matrices
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 03 June 2021, pp. 431-446
- Print publication:
- June 2022
-
- Article
- Export citation
Exponentials of de Branges–Rovnyak kernels
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 03 June 2021, pp. 447-455
- Print publication:
- June 2022
-
- Article
- Export citation
INJECTIVE LINEAR TRANSFORMATIONS WITH EQUAL GAP AND DEFECT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 18 May 2021, pp. 106-116
- Print publication:
- February 2022
-
- Article
- Export citation
DETERMINANTS AND PERMANENTS OF POWER MATRICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 17 May 2021, pp. 37-45
- Print publication:
- February 2022
-
- Article
- Export citation
1324- and 2143-avoiding Kazhdan–Lusztig immanants and k-positivity
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 14 May 2021, pp. 52-82
- Print publication:
- February 2023
-
- Article
- Export citation