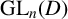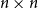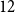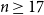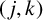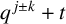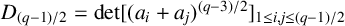Refine listing
Actions for selected content:
258 results in 15xxx
Products of commutators in matrix rings
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 14 January 2025, pp. 512-529
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spectral identities for Schrödinger operators
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 13 January 2025, pp. 484-491
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Product of two involutions in quaternionic special linear group
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 08 January 2025, pp. 421-439
- Print publication:
- June 2025
-
- Article
- Export citation
Full Poissonian local statistics of slowly growing sequences
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 24 March 2025, pp. 148-180
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Markov chain embedding problem in a one-jump setting
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 09 December 2024, pp. 674-696
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Completion problems and sparsity for Kemeny’s constant
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 20 November 2024, pp. 1-18
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LOCALLY NILPOTENT SUBGROUPS OF
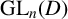 $\mathrm {GL}_n(D)$
$\mathrm {GL}_n(D)$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 06 November 2024, pp. 128-138
- Print publication:
- August 2025
-
- Article
- Export citation
Height functions on Hecke orbits and the generalised André–Pink–Zannier conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 19 November 2024, pp. 2531-2584
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A mathematical theory of super-resolution and two-point resolution
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 21 October 2024, e83
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cokernel statistics for walk matrices of directed and weighted random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 18 October 2024, pp. 131-150
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A CONJECTURE OF ZHI-WEI SUN ON MATRICES CONCERNING MULTIPLICATIVE SUBGROUPS OF FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 27 September 2024, pp. 490-496
- Print publication:
- June 2025
-
- Article
- Export citation
The full rank condition for sparse random matrices
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 20 September 2024, pp. 643-707
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A new formula for the determinant and bounds on its tensor and Waring ranks
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 18 September 2024, pp. 769-794
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CHARACTERISTIC POLYNOMIALS OF THE MATRICES WITH
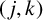 $(\,j,k)$-ENTRY
$(\,j,k)$-ENTRY 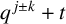 $q^{\,j\pm k}+t$
$q^{\,j\pm k}+t$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 03 June 2024, pp. 228-237
- Print publication:
- April 2025
-
- Article
- Export citation
Counting elements of the congruence subgroup
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 22 May 2024, pp. 955-969
- Print publication:
- December 2024
-
- Article
- Export citation
A reproducing kernel approach to Lebesgue decomposition
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 13 May 2024, pp. 1570-1610
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INVERSE CONNECTION FORMULAE FOR GENERALISED BESSEL POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 25 April 2024, pp. 480-487
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON GENERALISED LEGENDRE MATRICES INVOLVING ROOTS OF UNITY OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 22 April 2024, pp. 199-210
- Print publication:
- October 2024
-
- Article
- Export citation
A generalization of immanants based on partition algebra characters
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 01 April 2024, pp. 1001-1010
- Print publication:
- December 2024
-
- Article
- Export citation
MAXIMAL SUBSEMIGROUPS OF INFINITE SYMMETRIC GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 29 January 2024, pp. 324-337
- Print publication:
- October 2024
-
- Article
- Export citation