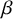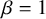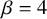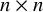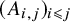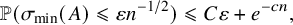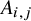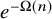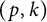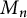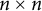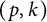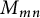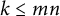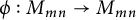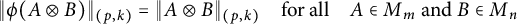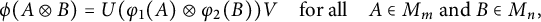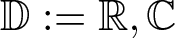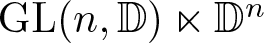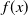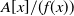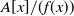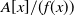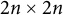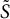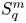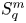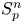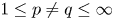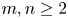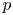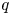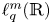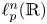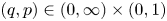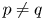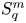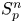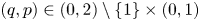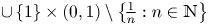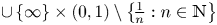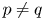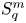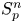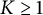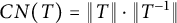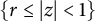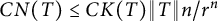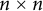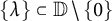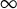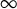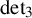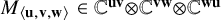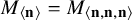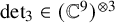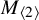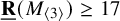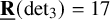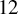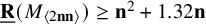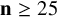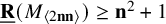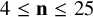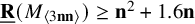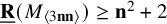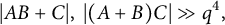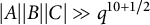Refine listing
Actions for selected content:
258 results in 15xxx
Asymptotic expansion of
 $\beta $ matrix models in the multi-cut regime
$\beta $ matrix models in the multi-cut regime
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 24 January 2024, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The least singular value of a random symmetric matrix
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 23 January 2024, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Linear maps preserving
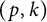 $(p,k)$-norms of tensor products of matrices
$(p,k)$-norms of tensor products of matrices
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 15 December 2023, pp. 187-207
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unified bounds for the independence number of graphs
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 11 December 2023, pp. 97-117
- Print publication:
- February 2025
-
- Article
- Export citation
The blowup-polynomial of a metric space: connections to stable polynomials, graphs and their distance spectra
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 09 November 2023, pp. 2073-2114
- Print publication:
- December 2024
-
- Article
- Export citation
Reversibility of affine transformations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 08 November 2023, pp. 1217-1228
-
- Article
- Export citation
Norms on complex matrices induced by random vectors II: extension of weakly unitarily invariant norms
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 447-457
- Print publication:
- June 2024
-
- Article
- Export citation
Autocorrelations of characteristic polynomials for the Alternative Circular Unitary Ensemble
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 27 October 2023, pp. 51-64
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Representatives of similarity classes of matrices over PIDs corresponding to ideal classes
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 18 October 2023, pp. 88-103
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SOME COUNTING QUESTIONS FOR MATRIX PRODUCTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 09 October 2023, pp. 32-43
- Print publication:
- August 2024
-
- Article
- Export citation
ON EXTERIOR POWERS OF REFLECTION REPRESENTATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 06 October 2023, pp. 90-102
- Print publication:
- August 2024
-
- Article
- Export citation
Block perturbation of symplectic matrices in Williamson’s theorem
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 15 August 2023, pp. 201-214
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Erdős–Ko–Rado theorem in Peisert-type graphs
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 04 August 2023, pp. 176-187
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Phase transition for the generalized two-community stochastic block model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 31 July 2023, pp. 385-400
- Print publication:
- June 2024
-
- Article
- Export citation
On isometric embeddability of $S_q^m$
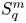 into $S_p^n$
into $S_p^n$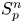 as non-commutative quasi-Banach spaces
as non-commutative quasi-Banach spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 22 June 2023, pp. 1180-1203
- Print publication:
- August 2024
-
- Article
- Export citation
LEFT AND RIGHT EIGENVECTORS OF A VARIANT OF THE SYLVESTER–KAC MATRIX
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 19 June 2023, pp. 316-326
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the condition number of a Kreiss matrix
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 29 May 2023, pp. 1376-1390
- Print publication:
- December 2023
-
- Article
- Export citation
New lower bounds for matrix multiplication and
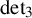 $\operatorname {det}_3$
$\operatorname {det}_3$
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 29 May 2023, e17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An energy decomposition theorem for matrices and related questions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 1280-1295
- Print publication:
- December 2023
-
- Article
- Export citation
Linear optimization over homogeneous matrix cones
- Part of
-
- Journal:
- Acta Numerica / Volume 32 / May 2023
- Published online by Cambridge University Press:
- 11 May 2023, pp. 675-747
-
- Article
-
- You have access
- Open access
- Export citation